吉林省2021年中考数学试卷
试卷更新日期:2021-07-20 类型:中考真卷
一、单选题
-
1. 化简 的结果为( )A、-1 B、0 C、1 D、22. 据《吉林日报》2021年5月14日报道,第一季度一汽集团销售整车70060辆,数据70060用科学记数法表示为( )A、 B、 C、 D、3. 不等式 的解集是( )A、 B、 C、 D、4. 如图,粮仓可以近似地看作由圆锥和圆柱组成,其主视图是( )
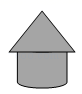 A、
A、 B、
B、 C、
C、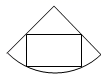 D、
D、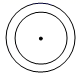 5. 如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为( )
5. 如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为( )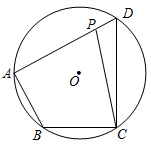 A、 B、 C、 D、6. 古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,若设这个数是 ,则所列方程为( )A、 B、 C、 D、
A、 B、 C、 D、6. 古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,若设这个数是 ,则所列方程为( )A、 B、 C、 D、二、填空题
-
7. 计算: -1= .8. 因式分解: .9. 计算: .10. 若关于 的一元二次方程 有两个相等的实数根,则 的值为 .11. 如图,已知线段 ,其垂直平分线 的作法如下:①分别以点 和点 为圆心, 长为半径画弧,两弧相交于 , 两点;②作直线 .上述作法中 满足的条作为 1.(填“ ”,“ ”或“ ”)
 12. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .
12. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .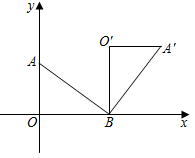 13. 如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
13. 如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 . 14. 如图,在 中, , , .以点 为圆心, 长为半径画弧,分别交 , 于点 , ,则图中阴影部分的面积为(结果保留 ).
14. 如图,在 中, , , .以点 为圆心, 长为半径画弧,分别交 , 于点 , ,则图中阴影部分的面积为(结果保留 ).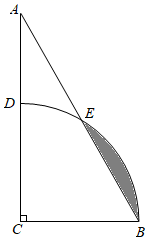
三、解答题
-
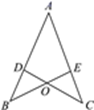
15. 先化简,再求值: ,其中 .16. 第一盒中有1个白球、1个黑球,第二盒中有1个白球,2个黑球.这些球除颜色外无其他差别,分别从每个盒中随机取出1个球,用画树状图或列表的方法,求取出的2个球都是白球的概率.17. 如图,点D在AB上,点E在AC上,BE和CD相交于点O , AB=AC , ∠B=∠C.求证:AD=AE
 18. 港珠澳大桥是世界上最长的跨海大桥,它由桥梁和隧道两部分组成,桥梁和隧道全长共 .其中桥梁长度比隧道长度的9倍少 .求港珠澳大桥的桥梁长度和隧道长度.19. 图①、图2均是 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点 ,点 均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
18. 港珠澳大桥是世界上最长的跨海大桥,它由桥梁和隧道两部分组成,桥梁和隧道全长共 .其中桥梁长度比隧道长度的9倍少 .求港珠澳大桥的桥梁长度和隧道长度.19. 图①、图2均是 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点 ,点 均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上. (1)、在图①中,以点 , , 为顶点画一个等腰三角形;(2)、在图②中,以点 , , , 为顶点画一个面积为3的平行四边形.20. 2020年我国是全球主要经济体中唯一实现经济正增长的国家,各行各业蓬勃发展,其中快递业务保持着较快的增长.给出了快递业务的有关数据信息.
(1)、在图①中,以点 , , 为顶点画一个等腰三角形;(2)、在图②中,以点 , , , 为顶点画一个面积为3的平行四边形.20. 2020年我国是全球主要经济体中唯一实现经济正增长的国家,各行各业蓬勃发展,其中快递业务保持着较快的增长.给出了快递业务的有关数据信息.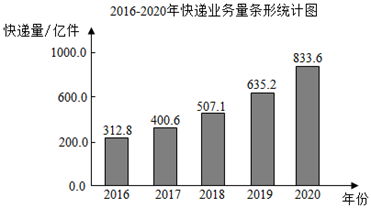
2016﹣2017年快递业务量增长速度统计表
年龄
2016
2017
2018
2019
2020
增长速度
51.4%
28.0%
26.6%
25.3%
31.2%
说明:增长速度计算办法为:增长速度=(本年业务量-去年业务量)÷去年业务量×100%.
根据图中信息,解答下列问题:
(1)、2016﹣2020年快递业务量最多年份的业务量是亿件.(2)、2016﹣2020年快递业务量增长速度的中位数是 .(3)、下列推断合理的是(填序号).①因为2016﹣2019年快递业务量的增长速度逐年下降,所以预估2021年的快递业务量应低于2020年的快递业务量;
②因为2016﹣2020年快递业务量每年的增长速度均在25%以上.所以预估2021年快递业务量应在 亿件以上.
21. 如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .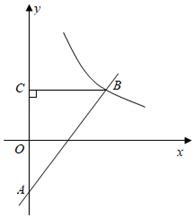 (1)、求反比例函数的解析式;(2)、求 的面积.22. 数学小组研究如下问题:长春市的纬度约为北纬 ,求北纬 纬线的长度,小组成员查阅了相关资料,得到三条信息:
(1)、求反比例函数的解析式;(2)、求 的面积.22. 数学小组研究如下问题:长春市的纬度约为北纬 ,求北纬 纬线的长度,小组成员查阅了相关资料,得到三条信息:⑴在地球仪上,与南,北极距离相等的大圆圈,叫赤道,所有与赤道平行的圆圈叫纬线;
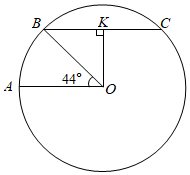
⑵如图, 是经过南、北极的圆,地球半径 约为 .弦 ,过点 作 于点 ,连接 .若 ,则以 为半径的圆的周长是北纬 纬线的长度;
⑶参考数据: 取3, , .
小组成员给出了如下解答,请你补充完整:
解:因为 , ,
所以 ( )(填推理依据),
因为 ,所以 ,
在 中, .
▲ (填“ ”或“ ”).
所以北纬 的纬线长
▲ (填相应的三角形函数值)
▲ ( )(结果取整数).
 23. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过 天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数 (万人)与各自接种时间 (天)之间的关系如图所示.
23. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过 天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数 (万人)与各自接种时间 (天)之间的关系如图所示.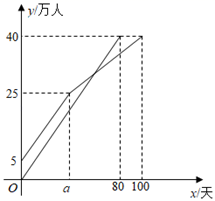 (1)、直接写出乙地每天接种的人数及 的值;(2)、当甲地接种速度放缓后,求 关于 的函数解析式,并写出自变量 的取值范围;(3)、当乙地完成接种任务时,求甲地未接种疫苗的人数.24. 如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .
(1)、直接写出乙地每天接种的人数及 的值;(2)、当甲地接种速度放缓后,求 关于 的函数解析式,并写出自变量 的取值范围;(3)、当乙地完成接种任务时,求甲地未接种疫苗的人数.24. 如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .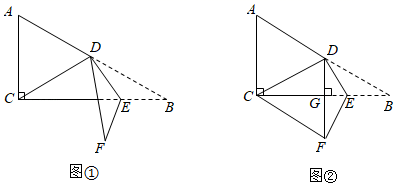 (1)、若 .直接写出 的长(用含 的代数式表示);(2)、若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如图②,判断四边形 的形状,并说明理由;(3)、若 ,直接写出 的度数.25. 如图,在矩形 中, , .动点 从点 出发沿折线 向终点 运动,在边 上以 的速度运动;在边 上以 的速度运动,过点 作线段 与射线 相交于点 ,且 ,连接 , .设点 的运动时间为 , 与 重合部分图形的面积为 .
(1)、若 .直接写出 的长(用含 的代数式表示);(2)、若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如图②,判断四边形 的形状,并说明理由;(3)、若 ,直接写出 的度数.25. 如图,在矩形 中, , .动点 从点 出发沿折线 向终点 运动,在边 上以 的速度运动;在边 上以 的速度运动,过点 作线段 与射线 相交于点 ,且 ,连接 , .设点 的运动时间为 , 与 重合部分图形的面积为 .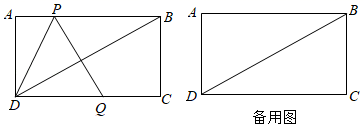 (1)、当点 与点 重合时,直接写出 的长;(2)、当点 在边 上运动时,直接写出 的长(用含 的代数式表示);(3)、求 关于 的函数解析式,并写出自变量 的取值范围.26. 如图,在平面直角坐标系中,二次函数 的图象经过点 ,点 .
(1)、当点 与点 重合时,直接写出 的长;(2)、当点 在边 上运动时,直接写出 的长(用含 的代数式表示);(3)、求 关于 的函数解析式,并写出自变量 的取值范围.26. 如图,在平面直角坐标系中,二次函数 的图象经过点 ,点 .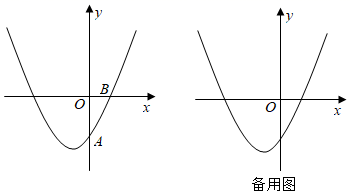 (1)、求此二次函数的解析式;(2)、当 时,求二次函数 的最大值和最小值;(3)、点 为此函数图象上任意一点,其横坐标为 ,过点 作 轴,点 的横坐标为 .已知点 与点 不重合,且线段 的长度随 的增大而减小.
(1)、求此二次函数的解析式;(2)、当 时,求二次函数 的最大值和最小值;(3)、点 为此函数图象上任意一点,其横坐标为 ,过点 作 轴,点 的横坐标为 .已知点 与点 不重合,且线段 的长度随 的增大而减小.①求 的取值范围;
②当 时,直接写出线段 与二次函数 的图象交点个数及对应的 的取值范围.