吉林省松原市乾安县2020-2021学年七年级下学期数学期中试卷

试卷更新日期：2021-07-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，计算正确的是（）

A、 $\pm \sqrt{16} = 4$ B、 $\sqrt{16} = \pm 4$ C、 $- \sqrt{16} = - 4$ D、 $\pm \sqrt{16} = \pm 8$

查看试题解析
2. 如图，四个图形中的∠1和∠2，不是同位角的是（）

A、 B、 C、 D、

查看试题解析
3. 在平面直角坐标系中，点P $(- 1 ， m^{2} + 1)$ 一定在（　　）．

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 在实数范围内，下列判断正确的是（）

A、若 $| m | = | n |$ ，则m=n B、若 $a^{2} > b^{2}$ ，则a＞b C、若 $\sqrt{a^{2}} = {(\sqrt{b})}^{2}$ ，则a=b D、若 $\sqrt[3]{a} = \sqrt[3]{b}$ ，则a=b

查看试题解析
5. 若方程组 ${\begin{array}{l} 4 x + 3 y = 14 \\ k x + (k - 1) y = 6 \end{array}$ 的解中x与y的值相等，则k为（）

A、4 B、3 C、2 D、1

查看试题解析
6. 如图，下列条件中，不能判断直线 $l_{1} / / l_{2}$ 的是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 2 = ∠ 3$ C、 $∠ 4 = ∠ 5$ D、 $∠ 2 + ∠ 4 = 180 °$

查看试题解析

二、填空题

7. 已知a、b为两个连续的整数，且 $a < \sqrt{28} < b$ ，则a+b= ．

查看试题解析
8. 实数 $a$ 、 $b$ 在数轴上对应点的位置如图所示，则化简 $\sqrt{a^{2}} - | a + b |$ 的结果为．

查看试题解析
9. 若 $x^{3 m - 3} - 2 y^{n - 1} = 5$ 是二元一次方程，则 $m^{n} =$ ．

查看试题解析
10. 已知点 $Q$ 的坐标为 $(2 a - 4 ， a + 4)$ ，且点 $Q$ 在 $x$ 轴上，则点 $Q$ 的坐标是．

查看试题解析
11.
如图所示，一个破损的扇形零件，利用图中的量角器可以量出这个扇形零件的圆心角的度数，测量的根据是

查看试题解析
12. 线段 $C D$ 是由线段 $A B$ 平移得到的，点 $A (- 1 ， 4)$ 的对应点为 $C (4 ， 7)$ ，则点 $D (1 ， 2)$ 的对应点 $B$ 的坐标为．

查看试题解析
13. 如图，将△ABC沿BC方向平移1cm得到△DEF ，若△ABC的周长等于10cm ，则四边形ABFD的周长等于．

查看试题解析
14. 把一张对边互相平行的纸条，折成如图所示， $E F$ 是折痕，若 $∠ E F B = 32 °$ ，则下列结论：（1） $∠ C' E F = 32 °$ ；（2） $∠ A E C = 148 °$ ；（3） $∠ B G E = 64 °$ ；（4） $∠ B F D = 116 °$ ．正确的有个．

查看试题解析

三、解答题

15. 计算：

(1)、 $| - \sqrt{9} | + \sqrt[3]{- 8} - \sqrt{\frac{1}{4}}$

(2)、求 $x$ 的值： ${(2 x - 1)}^{2} = 25$

查看试题解析
16. 已知 $4 a + 1$ 的平方根是 $\pm 3$ ， $b - 1$ 的算术平方根为2

(1)、求 $a$ 与 $b$ 的值；

(2)、求 $2 a + b - 1$ 的立方根.

查看试题解析
17. 有一个边长为9 cm的正方形和一个长为24 cm、宽为6 cm的长方形，要作一个面积为这两个图形的面积之和的正方形，问边长应为多少厘米？

查看试题解析
18. 如图，已知 $C D / / A B$ ，OE平分 $∠ B O D$ ， $OE ⊥ OF$ ， $∠ C D O = 62^{\circ}$ ，求 $∠ D O F$ 的度数。

查看试题解析
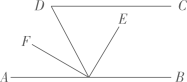19. 如图，正方形ABFG和正方形CDEF中，使点B、C的坐标分别为（0，0）和（4，0）．

(1)、在图中建立平面直角坐标系；

(2)、写出A点的坐标；

(3)、画出正方形EFCD左平移2个单位，上平移1个单位后的正方形E′F′C′D′．

查看试题解析
20. 如图，AD⊥BC于点D，EG⊥BC于点G，∠E=∠1．请问：AD平分∠BAC吗?若平分，请说明理由．

查看试题解析
21. 已知方程组 ${\begin{array}{l} a x + y = 15 \\ 4 x - b y = - 2 \end{array}$ 甲由于看错了方程（1）中的 $a$ ，得到方程组的解为 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ 是方程（2）的解；乙由于看错了方程（2）中的 $b$ ，得到方程组的解为 ${\begin{array}{l} x = 4 \\ y = 3 \end{array}$ 是方程（1）的解．若按正确的计算，求 $x + 6 y$ 的值．

查看试题解析
22. 如图，直线AB，CD相交于点O，OE平分 $∠ B O C$ ， $∠ F O D = 90 °$

(1)、若 $∠ A O F = 50 °$ ，求 $∠ B O E$ 的度数；

(2)、若 $∠ B O D$ ： $∠ B O E = 1$ ：4，求 $∠ A O F$ 的度数.

查看试题解析
23. 解方程组

(1)、 ${\begin{array}{l} x = y - 2 \\ 3 x + 2 y = - 1 \end{array}$

(2)、 ${\begin{array}{l} 2 x + y = 3 \\ 3 x - 5 y = 11 \end{array}$

查看试题解析
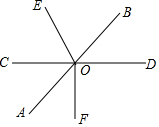24. 探究规律：我们有可以直接应用的结论：若两条直线平行，那么在一条直线上任取一点，无论这点在直线的什么位置，这点到另一条直线的距离均相等．例如：如图1，两直线 $m / / n$ ，两点 $H$ 、 $T$ 在 $m$ 上， $H E ⊥ n$ 于 $E$ ， $T F ⊥ n$ 于 $F$ ，则 $H E = T F$ ．
如图2，已知直线 $m / / n$ ， $A$ 、 $B$ 为直线 $n$ 上的两点， $C$ 、 $P$ 为直线 $m$ 上的两点．

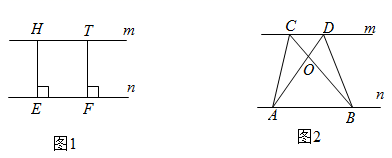(1)、请写出图中面积相等的各对三角形：．

(2)、如果 $A$ 、 $B$ 、 $C$ 为三个定点，点 $P$ 在 $m$ 上移动，那么无论 $P$ 点移动到任何位置总有：与 $△ A B C$ 的面积相等；理由是：．

查看试题解析
25. 如图

(1)、问题发现
如图①，直线 $A B / / C D$ ， $E$ 是 $A B$ 与 $A D$ 之间的一点，连接 $B E$ ， $C E$ ，可以发现： $∠ B + ∠ C = ∠ B E C$ ，请你写出证明过程；

(2)、拓展探究
如果点 $E$ 运动到图②所示的位置，其他条件不变，求证： $∠ B + ∠ C = 360 ° - ∠ B E C$ ．

(3)、解决问题
如图③， $A B / / D C$ ， $∠ C = 120 °$ ， $∠ A E C = 80 °$ ，则 $∠ A =$ ．（直接写出结论，不用写计算过程）

查看试题解析
26. 如图1，在平面直角坐标系中，点 $A$ ， $B$ 的坐标分别为 $A (a ， 0)$ ， $B (n ， 0)$ ，且 $a$ 、 $n$ 满足 $| a + 2 | + \sqrt{5 - n} = 0$ ，现同时将点 $A$ ， $B$ 分别向上平移4个单位，再向右平移3个单位，分别得到点 $A$ ， $B$ 的对应点 $C$ ， $D$ ，连接 $A C$ ， $B D$ ， $C D$ ．

(1)、直接写出 $A$ 、 $B$ 、 $C$ 、 $D$ 四点的坐标： $A$ ()， $B$ ()， $C$ ()， $D$ ()；

(2)、连接 $O C$ ，求四边形 $O B D C$ 的面积；

(3)、如图2，若点 $P$ 是线段 $B D$ 上的一个动点，连接 $P C$ ， $P O$ ，当点 $P$ 在 $B D$ 上移动时（ $P$ 不与 $B$ 、 $D$ 重合）时， $∠ O P C$ 与 $∠ D C P$ 、 $∠ B O P$ 存在怎样的关系，并说明理由．

查看试题解析