广东省深圳市龙华区2020-2021学年八年级下学期数学期中试卷

试卷更新日期：2021-07-20 类型：期中考试

进入出卷网下载

一、单选题

1. 已知x＞y ，则下列不等式成立的是（）

A、3x＜3y B、x﹣3＜y﹣3 C、﹣2x＞﹣2y D、x+5＞y+5

查看试题解析
2. 下列各式由左边到右边的变形中，是分解因式的是 $($ $)$

A、 $a (x - y) = a x - a y$ B、 $x^{2} - 4 x + 3 = x (x - 4) + 3$ C、 $a^{2} - b^{2} = (a + b) (a - b)$ D、 $a^{2} + 1 = a (a + \frac{1}{a})$

查看试题解析
3. 龙华区正推行垃圾分类政策，下列垃圾分类标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 把二次三项式x²﹣5x﹣14分解因式，下列结果正确的是（）

A、 $(x + 2) (x + 7)$ ） B、 $(x - 2) (x - 7)$ C、 $(x - 2) (x + 7)$ D、 $(x + 2) (x - 7)$

查看试题解析
5. 下列说法：
①真命题的逆命题一定是真命题；②等腰三角形的高、中线、角平分线互相重合；③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等；④用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先要假设“这个三角形中每一个内角都大于60°”．其中，正确的说法有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在平面直角坐标系中，线段 $A B$ 的两个端点是 $A (1 ， 3)$ ， $B (2 ， 1)$ .将线段 $A B$ 沿某一方向平移后，若点 $A$ 的对应点 $A^{'}$ 的坐标为 $(- 2 ， 0)$ ，则点 $B$ 的对应点 $B^{'}$ 的坐标为（）

A、 $(- 3 ， 2)$ B、 $(- 1 ， - 3)$ C、 $(- 1 ， - 2)$ D、 $(0 ， - 2)$

查看试题解析
7. 某商品进价为700元，出售时标价为1100元，后由于商品积压，商店准备打折销售，但要保证利润率不低于10%，则至多可打（）

A、六折 B、七折 C、八折 D、九折

查看试题解析
8. 如图，锐角△ABC的两条高BD、CE相交于点O ，且CE＝BD ，若∠CBD＝20°，则∠A的度数为（）

A、20° B、40° C、60° D、70°

查看试题解析
9. 如图，在△ABC中，以点A为圆心，AC的长为半径作弧，与BC交于点E ，分别以点E ， C为圆心，大于 $\frac{1}{2}$ EC的长为半径作弧，两弧相交于点P ，作射线AP交BC于点D ．若∠B＝45°，AC＝ $\sqrt{5}$ ，CD＝1，则AB的长度为（）

A、2 B、2 $\sqrt{2}$ C、2 $\sqrt{5}$ D、3 $\sqrt{2}$

查看试题解析
10. 如图，等边三角形ABC的边长为2，点O是△ABC的中心，∠FOG＝120°，将∠FOG绕点O旋转，分别交线段AB、BC于D、E两点，连接DE ，给出下列四个结论：①OD＝OE；②S_{四边形ODBE}＝ $\frac{1}{3}$ S_△ABC；③S_△ODE＝S_△BDE；④△BDE周长的最小值为3．上述结论中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

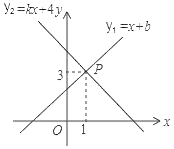
11. 若分式 $\frac{x - 1}{x}$ 的值为0，则 $x$ 的值为.

查看试题解析
12. 已知实数x，y满足 $| x - 6 | + \sqrt{3 - y} = 0$ ，则以x，y的值为两边长的等腰三角形的周长是．

查看试题解析
13. 如图，一次函数y₁＝x+b与一次函数y₂＝kx+4的图象交于点P（1，3），则关于x的不等式x+b＞kx+4的解集是.

查看试题解析
14. 如图所示，已知△ABC的周长是20，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是．

查看试题解析
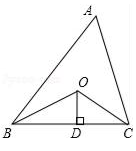15. 如图，过边长为3的等边△ABC的边AB上一点P ，作PE⊥AC于E ， Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D ，则DE的长为．

查看试题解析

三、解答题

16. 计算： $\frac{x + 2}{x^{2} - 6 x + 9} \div \frac{1}{3 - x} \cdot \frac{x - 3}{x + 2}$ ．

查看试题解析
17.

(1)、分解因式：﹣ax²+6ax﹣9a ．

(2)、解不等式组 ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 1 < 3 (x + 1) \end{array}$ ，并把其解集在数轴上表示出来．

查看试题解析
18. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．

(1)、①请画出将△ABC向左平移4个单位长度后得到的图形△A₁B₁C₁；
②请画出△ABC关于原点O成中心对称的图形△A₂B₂C₂；

(2)、在x轴上找一点P ，使△PAB的周长最小，请直接写出点P的坐标．

查看试题解析
19. 已知：如图，在△ADC中，AD＝CD ，且AB∥DC ， CB⊥AB于B ， CE⊥AD交AD的延长线于E ，连接BE ．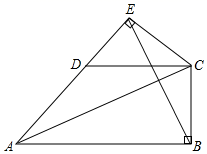

(1)、求证：CE＝CB；

(2)、若∠CAE＝30°，CE＝2，求BE的长度．

查看试题解析
20. 龙华区某学校组织400名师生春游，计划租用7辆客车，现有甲、乙两种型号客车，它们的载客量和租金如表．

甲种客车

乙种客车

载客量（座/辆）

70

45

租金（元/辆）

600

480

(1)、设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；（不要求写出x的取值范围）

(2)、如何租车能保证所有的师生可以参加春游且租车费用最少，最少费用是多少元？

查看试题解析
21. 如图1，已知直线y＝﹣2x+2与y轴、x轴分别交于A、B两点，以B为直角顶点在第一象限内作等腰Rt△ABC ．

(1)、A（）；B（）；

(2)、求BC所在直线的函数关系式；

(3)、如图2，直线BC交y轴于点D ，在直线BC上取一点E ，使AE＝AC ， AE与x轴相交于点F ．
①求证：BD＝ED；

②在直线AE上是否存在一点P ，使△ABP的面积等于△ABD的面积？若存在，直接写出点P的坐标；若不存在，说明理由．

查看试题解析
22. 如图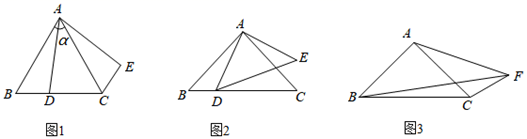

(1)、[问题背景]如图1，在△ABC中，AB＝AC ， ∠BAC＝α°，D为BC边上一点（不与点B、C重合）将线段AD绕点A逆时针旋转α°得到AE ，连接EC ，则∠BCE＝°（用含α的式子表示），线段BC ， DC ， EC之间满足的等量关系式为；

(2)、[探究证明]如图2，在Rt△ABC中，AB＝AC ， D为BC边上一点（不与点B、C重合）将线段AD绕点A逆时针旋转90°得到线段AE ，连接DE ，求证：BD²+CD²＝2AD²；

(3)、[拓展延伸]如图3，在四边形ABCF中，∠ABC＝∠ACB＝∠AFC＝45°，BF＝3，CF＝1．将△ABF绕点A逆时针旋转90°，试画出旋转后的图形，并求出AF的长度．（不要求尺规作图）

查看试题解析

	甲种客车	乙种客车
载客量（座/辆）	70	45
租金（元/辆）	600	480