广东省深圳市龙岗区2020-2021学年八年级下学期数学期中试卷
试卷更新日期:2021-07-20 类型:期中考试
一、单选题
-
1. 2021年3月,华为在深圳发布《华为创新和知识产权白皮书2020》,华为对遵循5G标准的单台手机专利许可费不高于2.5美元,则下面表示专利许可费 的不等关系正确的是( )A、 B、 C、 D、2. 下列交通标志中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知 ,下列不等式中,变形正确的是( ).A、 B、 C、 D、4. 下列等式中,从左到右的变形是因式分解的是( )A、2x(x-1)=2x2-2x B、x2-2x+3=x(x-2)+3 C、(x+y)2=x2+2xy+y2 D、-x2+2x=-x(x-2)5. 不等式组 的解集在数轴上表示正确的是( )A、
3. 已知 ,下列不等式中,变形正确的是( ).A、 B、 C、 D、4. 下列等式中,从左到右的变形是因式分解的是( )A、2x(x-1)=2x2-2x B、x2-2x+3=x(x-2)+3 C、(x+y)2=x2+2xy+y2 D、-x2+2x=-x(x-2)5. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、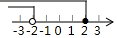 C、
C、 D、
D、 6. 在一次绿色环保知识竞赛中,共有20道题,对于每一道题,答对得10分,答错或不答扣5分,则至少答对多少题,得分才不低于80分?设答对 题,可列不等式为A、 B、 C、 D、7. 下列说法,正确的是( )A、一个三角形两边的垂直平分线的交点到这个三角形三边的距离相等 B、“若 ,则 ”的逆命题是真命题 C、在角的内部到角的两边距离相等的点一定在这个角的平分线上 D、用反证法证明“三角形中必有一个角不大于 ”,先假设这个三角形中有一个内角大于8. 如图,在 中, , ,尺规作图如下:分别以点 、点 为圆心,大于 为半径作弧,连接两弧交点的直线交 于点 ,连接 ,则 的度数为( )
6. 在一次绿色环保知识竞赛中,共有20道题,对于每一道题,答对得10分,答错或不答扣5分,则至少答对多少题,得分才不低于80分?设答对 题,可列不等式为A、 B、 C、 D、7. 下列说法,正确的是( )A、一个三角形两边的垂直平分线的交点到这个三角形三边的距离相等 B、“若 ,则 ”的逆命题是真命题 C、在角的内部到角的两边距离相等的点一定在这个角的平分线上 D、用反证法证明“三角形中必有一个角不大于 ”,先假设这个三角形中有一个内角大于8. 如图,在 中, , ,尺规作图如下:分别以点 、点 为圆心,大于 为半径作弧,连接两弧交点的直线交 于点 ,连接 ,则 的度数为( ) A、 B、 C、 D、9. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、 B、 C、 D、9. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( ) A、10 B、7 C、5 D、410. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( )
A、10 B、7 C、5 D、410. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 分解因式:a2+3a= .12. 已知等腰三角形其中一个内角为70°,则这个等腰三角形的顶角度数为.13. 某商店对一商品进行促销活动,将定价为10元的商品,按以下方式优惠销售:若购买不超过5件按原价付款;若一次性购买5件以上,超过部分打8折,现有98元钱,最多可以购买该商品件.14. 如图,已知函数 和 的图像交于点P,点P的横坐标为1,则关于x的不等式 的解集是 .
 15. 如图,在Rt△ABC中,∠C=90°,BC=2 ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为 .
15. 如图,在Rt△ABC中,∠C=90°,BC=2 ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为 .
三、解答题
-
16. 因式分解:(1)、(2)、17. 解不等式(组):(1)、(2)、18. 按要求画图及填空:在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点 及 的顶点都在格点上.
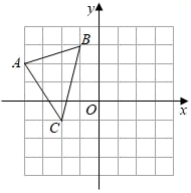 (1)、图中线段 的长度为 .(2)、将 先向下平移2个单位长度,再向右平移5个单位长度得到 ,画出 ;(3)、将 绕点 逆时针旋转 ,画出旋转后得到的 ,直接写出点 、 的坐标.19. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)、图中线段 的长度为 .(2)、将 先向下平移2个单位长度,再向右平移5个单位长度得到 ,画出 ;(3)、将 绕点 逆时针旋转 ,画出旋转后得到的 ,直接写出点 、 的坐标.19. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.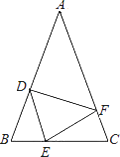 (1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数;20. 如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为点E,F,DB=DC.
(1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数;20. 如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为点E,F,DB=DC. (1)、求证:BE=CF;(2)、如果BD//AC,∠DAF=15°,求证:AB=2DF.21. 某公司在疫情复工准备工作中,为了贯彻落实“生命重于泰山、疫情就是命令、防控就是责任”的思想,计划同时购买一定数量的甲、乙品牌消毒液,若购进甲品牌消毒液20瓶和乙品牌消毒液10瓶,共需资金1300元;若购进甲品牌消毒液10瓶和乙品牌消毒液10瓶,共需资金800元.(1)、甲、乙品牌消毒液的单价分别是多少元?(2)、该公司计划购进甲、乙品牌消毒液共50瓶,而可用于购买这两种商品的资金不超过1900元,且要求购买甲品牌消毒液的数量不少于乙品牌消毒液数量的一半.试问:该公司有哪几种购买方案?哪种方案花费资金最少?22. 如图1,在平面直角坐标系中,直线 与 轴、 轴相交于 、 两点,动点 在线段 上,将线段 绕着点 顺时针旋转 得到 ,此时点 恰好落在直线 上时,过点 作 轴于点 .
(1)、求证:BE=CF;(2)、如果BD//AC,∠DAF=15°,求证:AB=2DF.21. 某公司在疫情复工准备工作中,为了贯彻落实“生命重于泰山、疫情就是命令、防控就是责任”的思想,计划同时购买一定数量的甲、乙品牌消毒液,若购进甲品牌消毒液20瓶和乙品牌消毒液10瓶,共需资金1300元;若购进甲品牌消毒液10瓶和乙品牌消毒液10瓶,共需资金800元.(1)、甲、乙品牌消毒液的单价分别是多少元?(2)、该公司计划购进甲、乙品牌消毒液共50瓶,而可用于购买这两种商品的资金不超过1900元,且要求购买甲品牌消毒液的数量不少于乙品牌消毒液数量的一半.试问:该公司有哪几种购买方案?哪种方案花费资金最少?22. 如图1,在平面直角坐标系中,直线 与 轴、 轴相交于 、 两点,动点 在线段 上,将线段 绕着点 顺时针旋转 得到 ,此时点 恰好落在直线 上时,过点 作 轴于点 .

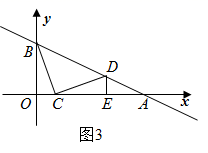 (1)、求证: ;(2)、求经过 、 两点的一次函数表达式.如图2,将 沿 轴正方向平移得 ,当直线 经过点 时,求点 的坐标及 的面积;(3)、在 轴上是否存在点 ,使得以 、 、 为顶点的三角形是等腰三角形?若存在,请写出 点的坐标.
(1)、求证: ;(2)、求经过 、 两点的一次函数表达式.如图2,将 沿 轴正方向平移得 ,当直线 经过点 时,求点 的坐标及 的面积;(3)、在 轴上是否存在点 ,使得以 、 、 为顶点的三角形是等腰三角形?若存在,请写出 点的坐标.