上海市金山区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，是一次函数的是（）

A、y＝1﹣x B、y＝ $\frac{1}{x}$ C、y＝kx＋1 D、y＝x²＋1

查看试题解析
2. 如果关于x的方程ax＝b无解，那么a、b满足的条件（）

A、a＝0，b＝0 B、a≠0，b≠0 C、a≠0，b＝0 D、a＝0，b≠0

查看试题解析
3. 下列一次函数中函数值y随x的增大而减小的是（）

A、y＝2x＋1 B、y＝2x﹣1 C、y＝1﹣2x D、y＝ $\frac{1}{2}$ x﹣1

查看试题解析
4. 下列事件：①第十届中国花卉博览会闭幕日（2021年7月2日）当天现场是晴天；②在直角坐标系中一次函数的图象一定是直线；③平面上任意画一个凸多边形，它的内角和一定是180°的倍数；④掷一骰了，点数为偶数的面朝上．其中属于确定事件的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 平面内有三个不同的点A、B、C ， $\vec{A B} + \vec{B C} + \vec{C A}$ 的结果是（）

A、0 B、 $\vec{0}$ C、1 D、单位向量

查看试题解析
6. 在四边形ABCD中，AD∥BC ，添加下列选项中的一个条件，不能得到四边形ABCD是平行四边形，这个选项是（）

A、AD＝BC B、AB∥CD C、AB＝CD D、∠A＝∠C

查看试题解析

二、填空题

7. 在直角坐标系中，直线l与直线y＝﹣x＋2平行，且截距为3，那么直线l的表达式是．

查看试题解析
8. 在直角坐标系中，一次函数y＝ $\frac{1}{2}$ x﹣1的图像不经过第象限．

查看试题解析
9. 直线y＝﹣2x＋3向上平移3个单位后，所得线的函数表达式是．

查看试题解析
10. 方程 $\sqrt{3 - x}$ ﹣1＝0的解是．

查看试题解析
11. 方程组 ${\begin{array}{l} x + y = 3 \\ x y = 2 \end{array}$ 的根是

查看试题解析
12. 布袋里有3个黄球、4个白球，5个绿球，它们除色外其它都相同，从布袋里摸出一个球恰好是白球的概率是．

查看试题解析
13. 从2、6、9三个数字中任选两个，用这两个数字分别作为十位数和个位数组成一个两位数，在所有得到的两位数中随机抽取一个两位数，这个两位数是4的倍数的概率是．

查看试题解析
14. 如果一个正多边形的一个外角是60°，那么这个正多边形的边数是.

查看试题解析
15. 如图，在▱ABCD中，DE平分∠ADC ，交BC于点E ， BE＝3，EC＝5，那么▱ABCD的周长等于．

查看试题解析
16. 如果菱形的一条对角线长是另一条长的 $\sqrt{3}$ 倍，这个菱形的面积等6 $\sqrt{3}$ ，那么这个菱形的周长等于．

查看试题解析
17. 如图，正方形ABCD的边长等于4，对角线AC、BD相交于点O ， E是DB延长线上一点，∠BCE＝15°，那么△BCE的面积等于．

查看试题解析
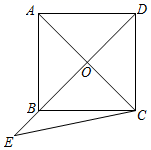18. 如图，已知矩形ABCD中AB＝3，BC＝5，E是的边CD上一点，将△ADE沿直线AE翻折后，点D恰好落在边BC上的点F处，那么DE的长为．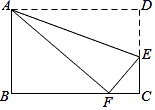

查看试题解析

三、解答题

19. 解方程：x﹣ $\sqrt{2 x - 1}$ ＝2

查看试题解析
20. 解方程组： ${\begin{matrix} \frac{1}{x - 2} - \frac{2}{y + 3} = 1 \\ \frac{3}{x - 2} + \frac{1}{y + 3} = 10 \end{matrix}$ ．

查看试题解析
21. 已知：一次函数y＝（m﹣2）x＋4的图像经过点A（2，6）且与x轴相交于点B ．

(1)、求一次函数的解析式；

(2)、求△AOB的面积．

查看试题解析
22. 如图，已知点E在行四边形ABCD的边CD上，设 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$ ， $\vec{D E} = \vec{c}$ ．图中的线段都成有向线段．

(1)、用 $\vec{a}$ 、 $\vec{b}$ 、 $\vec{c}$ 的式子表示： $\vec{A E}$ ＝， $\vec{B E}$ ＝．

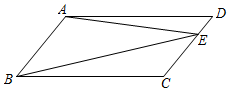(2)、在图中求作 $\vec{B C} + \vec{C E} - \vec{A B}$ （不写作法，保留作图痕迹）．

查看试题解析
23. 已知：如图四边形ABCD是菱形，E是对角线BD上的一点，联结AE、CE ．求证：∠DAE＝∠DCE ．

查看试题解析
24. 已知：如图，点O是△ABC内一点，D、E、F、G分别是OB、OC、AC、AB的中点．

(1)、求证：四边形DEFG是平行四边形；

(2)、如果AB＝AC ， OB＝OC ，求证：四边形DEFG是矩形．

查看试题解析
25. 在2021“五五购物节”中，某商店的两种品牌的小电器参与促销活动．经统计后发现，每天的销售中，乙品牌小电器的销售数量y（件）与甲品牌小电器的销售量x（件）符合如图表示的函数关系．

(1)、求y关于x的函数解析式（不必写出自变量x的取值范围）；

(2)、在5月2日一天的销售中，甲、乙两种品牌的小电器的销售额分别为1200元和1440元，已知甲品牌的小电器单价比乙品牌的小电器单价多20元，求甲、乙两种品牌的小电器的单价．（其中小电器的单价大于100元）

查看试题解析
26. 如图，已知在梯形ABCD中，AD∥BC ， ∠ABC＝∠BCD＝45°，BC＝8，DE⊥BC ，垂足为E ，延长DE至F ，使得DE＝EF ，联结AC、BF、CF ．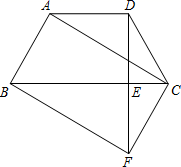

(1)、求证：四边形ABFC是平行四边形；

(2)、设AD＝x ，梯形ABCD的面积为y ，求y关于x的函数关系式，并写出自变量x的取值范围；

(3)、联结AF交BC于点O ，如果△AOB是等腰三角形，求AD的长．

查看试题解析