天津市和平区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. ${(- 7)}^{2}$ 的算术平方根是（）

A、7 B、－7 C、±7 D、 $\sqrt{7}$

查看试题解析
2. 下列各选项的结果表示的数中，不是无理数的是（）

A、如图，直径为单位1的圆从数轴上的原点沿着数轴无滑动地顺时针滚动一周到达点A，点A表示的数 B、5的算术平方根 C、9的立方根 D、 $\sqrt{144}$

查看试题解析
3. 下列调查中，调查方式选择合理的是（）

A、为了了解某一品牌家具的甲醛含量，选择全面调查 B、为了了解某公园的游客流量，选择抽样调查 C、为了了解神舟飞船的设备零件的质量情况，选择抽样调查 D、为了了解一批袋装食品是否有防腐剂，选择全面调查

查看试题解析
4. 已知点P(x，y)的坐标满足|x|=3， $\sqrt{y}$ =2，且xy＜0，则点P的坐标是（）

A、 $(3 ， - 2)$ B、 $(- 3 ， 2)$ C、 $(3 ， - 4)$ D、 $(- 3 ， 4)$

查看试题解析
5. 如图，给出下列四个条件：① $∠ B + ∠ B A D = 180 °$ ；② $∠ 1 = ∠ 2$ ；③ $∠ B = ∠ 5$ ；④ $∠ 3 = ∠ 4$ ．其中能判定 $A B // C D$ 的条件有（）

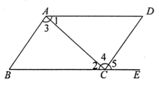A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，A ， B的坐标为（2，0），（0，1），若将线段AB平移至A₁B₁ ，点A对应点A₁（3，b），点B对应点B₁（a ， 3），则a+b的值为（）

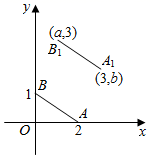A、－1 B、1 C、3 D、5

查看试题解析
7. 下列不等式变形不一定成立的是（）

A、若 $a > b$ ，则 $a + c > b + c$ B、若 $a + c > b + c$ ，则 $a > b$ C、若 $a > b$ ，则 $a c^{2} > b c^{2}$ D、若 $a > b$ ，则 $1 + a > b - 1$

查看试题解析
8. 甲、乙两人在解方程组 $\{\begin{cases} a x + 5 y = 15 ① \\ 4 x = b y - 2 ② \end{cases}$ 时，甲看错了方程①中的a ，解得 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ ，乙看错了方程②中的 b ，解得 ${\begin{matrix} x = 5 \\ y = 4 \end{matrix}$ ，则 $a^{2019} - {(- \frac{b}{10})}^{2020}$ 的值为（）

A、2 B、－2 C、0 D、－3

查看试题解析
9. 在矩形ABCD中，放入六个形状、大小相同的长方形，所标尺寸如图所示，设小长方形的长、宽分别为xcm，ycm，则下列方程组正确的是（）

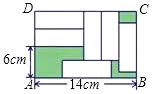A、 ${\begin{array}{l} x - 2 y + y = 6 \\ x + 3 y = 14 \end{array}$ B、 ${\begin{array}{l} x + 3 y = 14 \\ x + 2 y = 6 \end{array}$ C、 ${\begin{array}{l} x + 3 y = 14 \\ 2 x - y = 6 \end{array}$ D、 ${\begin{cases} x + 3 y = 14 \\ x + y = 6 \end{cases}$

查看试题解析
10. 下列命题：①过一点有且只有一条直线垂直于已知直线；②两条平行线被第三条直线所截，同位角的平分线互相平行；③点P为直线l外一点，点A、B、C为直线l上的三点，PA=2 $c m$ ，PB=3 $c m$ ，PC=4 $c m$ ，那么点P到直线l的距离是2 $c m$ ；④ $∠ β$ 与 $∠ α$ 的两边分别平行， $∠ β$ 比 $∠ α$ 的3倍少40°，则 $∠ β$ =125°；是真命题的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 三个连续正整数之和小于333，这样的正整数有（）

A、111组 B、110组 C、109组 D、108组

查看试题解析
12. 关于x ， y的，二元一次方程(a-1)x+ (a+2)y+5-2a=0 ，当a取一个确定的值时就得到一个方程，所有这些方程有一个公共解，则这个公共解是（）

A、 ${\begin{matrix} x = 3 \\ y = 5 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = 0 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ D、 ${\begin{cases} x = 3 \\ y = - 1 \end{cases}$

查看试题解析

二、填空题

13. 若 $\sqrt{3} \approx 1.732$ ， $\sqrt{30} \approx 5.477$ ，则 $\sqrt{3000} \approx =$ ．

查看试题解析
14. 从鱼池的不同地方捞出100条鱼，在鱼的身上做上记号，然后把鱼放回鱼池.过一段时间后，在同样的地方再捞出50条鱼，其中带有记号的鱼有2条，则可以估计整个鱼池约有鱼条.

查看试题解析
15. 如图，已知AD//BC ， BD平分∠ABC ， ∠A＝112°，且BD⊥CD ，则∠ADC＝．

查看试题解析
16. 在等式 y=ax²+bx+c 中，当 x=-1 时， y=0 ；当 x=2 ， y=3 ；当 x=5 时， y=60 ，则a= ， b= ， c= ．

查看试题解析
17. 已知关于x的不等式组 ${\begin{array}{l} 2 x - m < 0 \\ x > - 4 \end{array}$ 有解，则m的取值范围为．

查看试题解析
18. 如图，在每个小正方形的边长为1的网格中．

(1)、如图，线段AB ， CD的端点A ， B ， C ， D均在格点上，请直接写出线段AB与CD的关系；

(2)、如图，线段AB ， AD ， BC的端点均在格点上，线段BC与AD相交于点P ，请用无刻度的直尺，过点P作直线PQ平行AB ．

查看试题解析

三、解答题

19. 解方程组 ${\begin{matrix} \frac{2 (x - y)}{3} - \frac{x + y}{4} = - 4 ① \\ 6 (x + y) - 4 (2 x - y) = 16 ② \end{matrix}$ ．

查看试题解析
20. 解不等式组 $\{\begin{cases} x - 3 (x - 2) \leq 4 ① \\ \frac{1 + 2 x}{3} > x - 1 ② \end{cases}$ ．
请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组的解集为．

查看试题解析
21. 学校在暑假期间开展“心怀感恩，孝敬父母”的实践活动，倡导学生在假期中帮助父母干家务．开学以后，校学生会随机抽取了部分学生，对暑假“平均每天帮助父母干家务所用时长”进行了调查，根据统计数据，绘制出如下的统计图（每段时长均含有最小值，不含最大值）．

根据上述信息，回答下列问题：

(1)、在本次随机抽取的样本中，调查的学生人数为；

(2)、补全频数分布直方图；

(3)、图②中m的值为；

(4)、求图②表示平均每天帮助父母干家务30—40分钟的扇形所对的圆心角的度数；

(5)、如果该校共有学生2000人，请你估计“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有多少人？

查看试题解析
22. 如图，AD平分 $∠ B D A + ∠ C E G = 180 °$ 交BC于点D ，点F在BA的延长线上，点E在线段CD上，连接EF与AC相交于点G 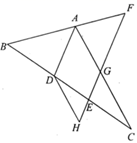， $∠ B D A + ∠ C E G = 180 °$ ．

（Ⅰ）AD与EF平行吗？请说明理由；

（Ⅱ）若点H在FE的延长线上，且 $∠ E D H = ∠ C$ ，试探究 $∠ F$ 与 $∠ H$ 的数量关系，请说明理由．

查看试题解析
23. 经销商销售甲型、乙型两种产品，价格随销售量 $a$ 的变化而不同，具体如下表：

已知销售10件甲型产品和30件乙型产品的销售额为750元，销售60件甲型产品和100件乙型产品的销售额为2520元．

(1)、求 a 、 b 的值；

(2)、若学校要购买甲型、乙型两种产品共101件，购买的甲产品少于乙产品，所用经费不超过1680元，则有多少种购买方案．

查看试题解析
24. 已知关于x ， y的方程满足方程组 ${\begin{array}{l} 3 x + 2 y = m + 1 ① \\ 2 x + y = m - 1 ② \end{array}$ ，
（Ⅰ）若 x-y=2 ，求m的值；

（Ⅱ）若x ， y ， m均为非负数，求m的取值范围，并化简式子 $| m - 3 | + | m - 5 |$ ；

（Ⅲ）在（Ⅱ）的条件下求 $s = 2 x - 3 y + m$ 的最小值及最大值．

查看试题解析
25. 如图，在平面直角坐标系中，已知点A(a，0) $B (0 ， b)$ ，．
（Ⅰ）如图，若 $| a + b + 1 | + \sqrt{3 a + 4 b} = 0$ ，已知点 $C (m ， - m)$ ．

①连接AC ，当 $A C // y$ 轴时，求m的值：

②若 $△ A B C$ 的面积是8，求m的值：

（Ⅱ）如图，若 $∠ A B O = 60 °$ ，射线BA以每秒9°的速度绕点B顺时针方向旋转至射线BA₁ ，点M为x轴正半轴上一点，射线MO以每秒6°的速度绕点M逆时针方向旋转到MO₁ ，设运动时间为t秒 $(0 < t < 30)$ ，求t为多少秒时，直线 $B A_{1} // M O_{1}$ ？

查看试题解析