山东省济南市天桥区2020-2021学年七年级下学期数学期末试卷
试卷更新日期：2021-07-20 类型：期末考试
一、单选题
-
1. 下面的图形是用数学家名字命名的，其中是轴对称图形的是：（ ）A、
B、
C、
D、
2. 新型冠状病毒非常小，其半径约为0.0000016m，用科学记数法可以表示为：（ ）A、1.6×10－6m B、1.6×10－7m C、1.6×107m D、1.6×10－8m3. 下列事件中是不确定事件的是（ ）A、某同学立定跳远成绩为20米 B、一个袋中只装有5个红球，摸出一个红球 C、明天太阳从西边升起来 D、济南市明年十月一日是晴天4. 下列计算的结果为 的是：（ ）A、 B、 C、 D、5. 在圆的周长公式C=2πr中，下列说法正确的是（ ）A、C，π，r是变量，2是常量 B、C，π是变量，2，r是常量 C、C，r是变量，2，π是常量 D、以上都不对6. 下列长度的三条线段，能组成三角形的是（ ）A、2，3，4 B、2，3，5 C、2，2，4 D、2，2，57. 如图，测河两岸A，B两点的距离时，先在AB的垂线BF上取C，D两点，使CD＝BC，再过点D画出BF的垂线DE，当点A，C，E在同一直线上时，可证明△EDC≌△ABC，从而得到ED＝AB，测得ED的长就是A，B的距离，判定△EDC≌△ABC的依据是：（ ）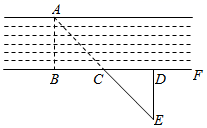
A、ASA B、SSS C、AAS D、SAS8. 如图，将长方形ABCD沿直线l折叠使得点B落在点E，点C落在点F处，若∠AGE＝70°，那么∠GHE的度数是：（ ）
A、70° B、60° C、65° D、55°9. 某林业局将一种树苗移植成活的情况绘制成如下统计图，由此可估计这种树苗移植成活的概率约为（ ）
A、0.95 B、0.90 C、0.85 D、0.8010. 如图，一棵树从3m处折断了，树顶端离树底端距离4m，那么这棵树原来的高度是：（ ）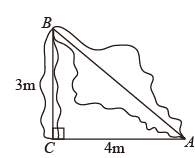
A、8m B、5m C、9m D、7m11. 如图所示，在正方形网格中，点A、B、C、D、E、F是网格线交点；直线l经过点A、B、C、D、如果在直线l上存在一点M，使得ME＋MF的值最小，则点M在（ ）
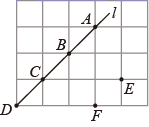A、点A B、点B C、点C D、点D12. 甲、乙两车分别从A、B两地同时出发，相向而行，匀速行驶，甲车以60km/h的速度行驶，在这个过程中，两车之间的距离y与甲车行驶的时间t之间的关系如图所示，那么下列说法错误的是：（ ）
A．
A、B两地相距280km B、a＝ C、b＝ D、c＝220二、填空题
-
13. 计算： .14. 在一个不透明的盒子里，装有10个红球和5个蓝球，每个球除颜色外都相同，从中任意摸出一个球，摸到蓝球的概率是.15. 直角三角形两锐角的度数分别为x，y，其关系式为y＝90－x，当y＝43时，x＝；16. 如图，已知 ，若以“SAS”为依据证明 ，还要添加的条件 ．
17. 已知在(x＋a)(x＋b)＝x2＋mx－16中，a、b为整数，则m的值一共有种可能．18. 如图，△ABC中∠BAC＝60°，将△ACD沿AD折叠，使得点C落在AB上的点C′处，连接C′D与C′C，∠ACB的角平分线交AD于点E；如果BC′＝DC′；那么下列结论：①∠1＝∠2；②AD垂直平分C′C；③∠B＝3∠BCC′；④DC∥EC；其中正确的是：；(只填写序号)
三、解答题
-
19. 计算：(1)、(2)、│－2│－(2－π)0＋(－ )－120. 先化简，再求值：(x＋3)2－(x－1)(x－2)；其中x＝ ，21. 如图，在△ABC中，∠B＝80°，∠C＝30°，AD⊥BC于点D，AE平分∠BAC，求∠EAD的度数．
22. 如图，△ABC的顶点A、B、C都在边长为1的小正方形的格点上，请利用格点画图．
(1)、画△A1B1C1 ， 使它与△ABC关于直线l成轴对称：(2)、在直线l上找一点P，使点PA＝PB；(3)、△ABC的面积是：；23. 如图，点A，F，C，E在同一直线上，∠B＝∠D，BC＝DF，∠A＝∠E．请说明AF＝CE的理由，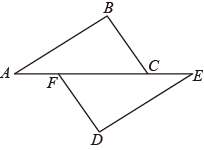
24. 小明和小亮在玩转盘游戏，如图所示，小明将一个转盘平均分成6份，并标上：1、2、3、4、5，转盘可以随意转动．
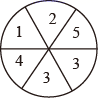(1)、请你求出指针指向3的倍数的概率；(2)、如果游戏规定，若指针指向偶数，则小明胜利；反之，则小亮胜利，你认为这个游戏公平吗？为什么？25. 已知：(x－1)(x＋1)＝x2－1(x－1)(x2＋x＋1)＝x3－1
(x－1)(x3＋x2＋x＋1)＝x4－1
(x－1)(x4＋x3＋x2＋x＋1)＝x5－1
(1)、当x＝3时，(3－1)×(33＋32＋3＋1)＝；……
(2)、试求：25＋24＋23＋22＋2＋1的值．(3)、判断22021＋22020＋22019＋……＋22＋2＋1的值的个位数是；26. 如图①，∠B＝∠C＝90°，点P从A出发，沿A－B－C－D路线运动，到D停止；点P的速度为每秒1cm，运动时间为x秒，如图②是△ABP的面积S(cm2)与x(秒)的图象．
(1)、图②中自变量是；因变量是；时间段内点P在线段BC上运动；(2)、根据题目中提供的信息，请你推断出图①中的AB＝cm；BC＝cm；CD＝cm；图②中的m＝cm2；(3)、当△ADP是以∠ADP为底角的等腰三角形时，求PB2的值，27. 已知△ABC和△ADE都是等边三角形，点D在射线BF上，连接CE．
(1)、如图1，BD与CE是否相等？请说明理由；(2)、如图1，求∠BCE的度数；(3)、如图2，当D在BC延长线上时，连接BE，△ABE、△CDE与△ADE的面积有怎样的关系？并说明理由．