山东省济南市槐荫区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个交通标志图中，为轴对称图形的是（　）

A、 B、 C、 D、

查看试题解析
2. 若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（）

A、1 B、2 C、3 D、8

查看试题解析
3. 如果“□ $\times 2 a b = 4 a^{2} b$ ”，那么“□”内应填的代数式是（）

A、 $2 a b$ B、 $2 a$ C、 $a$ D、 $2 b$

查看试题解析
4. 下列各式计算正确的是（）

A、 $x^{2} \cdot x^{3} = x^{6}$ B、 $3 x y^{2} - x y^{2} = 2 x y^{2}$ C、 ${(x + y)}^{2} = x^{2} + y^{2}$ D、 ${(2 x y^{2})}^{2} = 4 x y^{2}$

查看试题解析
5.
如图，∠1=∠2，则下列结论一定成立的是（　　）

A、AB//CD B、AD//BC C、∠B=∠D D、∠3=∠4

查看试题解析
6. 下列命题中是假命题的是（）

A、两直线平行，同位角互补 B、对顶角相等 C、直角三角形两锐角互余 D、平行于同一直线的两条直线平行

查看试题解析
7. 在下列多项式的乘法中，可以用平方差公式计算的是（）

A、 $(2 x + y) (2 y - x)$ B、 $(\frac{1}{2} x + 1) (- \frac{1}{2} x - 1)$ C、 $(3 x - y) (3 x + y)$ D、 $(x - y) (- x + y)$

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A D$ 平分 $∠ B A C$ ， $B C = 10$ ， $C D = 6$ ，则点D到AC的距离为（）

A、4 B、6 C、8 D、10

查看试题解析
9. 已知等腰三角形的两边长分别是 $4 cm$ 和 $8 cm$ ，则周长为（）

A、 $16 cm$ B、 $20 cm$ C、 $16 cm$ 或 $20 cm$ D、 $24 cm$

查看试题解析
10. 小华同学喜欢锻炼，周六他先从家跑步到新华公园，在那里与同学打一会羽毛球后又步行回家，下面能反映小华离家距离 $y$ 与所用时间 $x$ 之间关系的图象是（）

A、 B、 C、 D、

查看试题解析
11. 如图，△ABC是等边三角形，AQ=PQ ， PR⊥AB于点R ， PS⊥AC于点S ， PR=PS.下列结论：①点P在∠A的角平分线上；②AS=AR；③QP∥AR；④△BRP≌△QSP ．其中，正确的有（）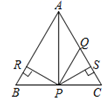

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1)$ … $(2^{32} + 1)$ +1 的个位数字为（）

A、2 B、4 C、6 D、8

查看试题解析

二、填空题

13. 在关系式 $y = 2 x$ 中，当自变量 $x = 3$ 时，因变量 $y$ 的值是．

查看试题解析
14. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为米.

查看试题解析
15. 如图，要测量水池宽 $A B$ ，可从点 $A$ 出发在地面上画一条线段 $A C$ ，使 $A C ⊥ A B$ ，再从点 $C$ 观测，在 $B A$ 的延长线上测得一点 $D$ ，使 $∠ A C D = ∠ A C B$ ，这时量得 $A D = 120 m$ ，则水池宽 $A B$ 的长度是 m．

查看试题解析
16. 若（x+2）（x﹣4）＝x²+nx﹣8，则n＝．

查看试题解析
17. 如图，以 $△ A B C$ 的顶点 $B$ 为圆心， $B A$ 长为半径画弧，交 $B C$ 边于点 $D$ ，连接 $A D$ ．若 $∠ B A C = 100 °$ ， $∠ C = 50 °$ ，则 $∠ B A D$ 的大小为度．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ B A C = 120 °$ ，分别作 $A C$ ， $A B$ 两边的垂直平分线 $P M$ 、 $P N$ ，垂足分别是点 $M$ 、 $N$ ．以下说法正确的是（填序号）．
① $∠ P = 60 °$ ；② $∠ E A F = ∠ B + ∠ C$ ；③ $P E = P F$ ；④点 $P$ 到点 $B$ 和点 $C$ 的距离相等．

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- 3)}^{2} - {(\frac{1}{2})}^{- 1}$

(2)、 $(4 m^{3} - 2 m^{2}) \div 2 m$

查看试题解析
20. 先化简，再求值： $(x + 5) (x - 1) + {(x - 2)}^{2}$ ，其中 $x = 4$ ．

查看试题解析
21. 已知：点 $B$ 、 $E$ 分别在 $A C$ 、 $D F$ 上， $B D$ 、 $C E$ 分别交 $A F$ 于点 $G$ 、 $H$ ， $∠ A G B = ∠ E H F$ ， $∠ C = ∠ D$ ．求证： $A C // D F$

查看试题解析
22. 如图，在长度为一个单位长度的小正方形组成的正方形网格中， $△ A B C$ 的顶点在小正方形的顶点上．

(1)、画出 $△ A B C$ 关于直线 $l$ 对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、求 $△ A B C$ 的面积；

(3)、在直线 $l$ 上找一点 $Q$ ，使点 $Q$ 到点 $B$ 与点 $C$ 的距离之和最小．

查看试题解析

23. 2020年，周至县小李家的猕猴桃喜获丰收．在销售过程中，猕猴桃的销售额y（元）与销量x（千克）满足如下关系：

销售量x（千克）	1	2	3	4	5	6	7	8
销售额y（元）	6	12	18	24	30	36	42	48

(1)、在这个变化过程中，自变量是，因变量是；

(2)、猕猴桃的销售额y（元）与销售量x（千克）之间的关系式为；

(3)、当猕猴桃销售量为100千克时，销售额是多少元？

查看试题解析

24. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ ， $E$ 在 $B C$ 上 $(B D < B E)$ ， $B D = C E$ .

(1)、求证： $△ A B D$ ≌ $△ A C E$ .

(2)、若 $∠ A D E = 2 ∠ B$ ， $B D = 2$ ，求 $A E$ 的长.

查看试题解析
25. 某机动车出发前油箱内有油42L，行驶若干小时后，途中在加油站加油若干升．油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据图回答问题：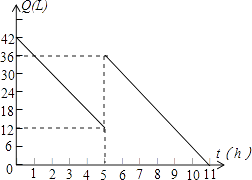

(1)、机动车行驶5h后加油，途中加油升；

(2)、根据图形计算，机动车在加油前的行驶中每小时耗油多少升？

(3)、如果加油站距目的地还有400km，车速为60km/h，要到达目的地，油箱中的油是否够用？请说明理由．

查看试题解析
26. 如图，在 $△ A B C$ 中， $D$ 为 $A B$ 的中点， $A B = A C = 10$ ， $B C = 8$ ，动点 $P$ 从点 $B$ 出发，沿 $B C$ 方向以3个单位长度每秒的速度向点 $C$ 运动；同时动点 $Q$ 从点 $C$ 出发，沿 $C A$ 方向以3个单位长度每秒的速度向点 $A$ 运动，运动时间是 $t$ 秒．

(1)、在运动过程中，当 $t =$ 秒时， $C P = C Q$ ；

(2)、在运动过程中，当 $△ B P D ≌ △ C Q P$ 时，求出 $t$ 的值；

(3)、是否存在某一时刻 $t$ ，使 $△ B P D ≌ △ C P Q$ ？若存在，求出 $t$ 的值；若不存在，请说明理由．

查看试题解析
27. 如图，在等边 $△ A B C$ 中，已知点 $E$ 在直线 $A B$ 上（不与点 $A$ 、 $B$ 重合），点 $D$ 在直线 $B C$ 上，且 $E D = E C$ ．

图1

图2

(1)、若点 $E$ 为线段 $A B$ 的中点时，求证： $D B = A E$ ；

(2)、若 $△ A B C$ 的边长为2， $A E = 1$ ．求 $C D$ 的长．

查看试题解析