北京市西城区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-07-20 类型:期末考试
一、单选题
-
1. 8的立方根是( )A、±2 B、2 C、﹣2 D、2. 已知实数a、b,若a>b,则下列结论正确的是A、 B、 C、 D、3. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点 .“馬”位于点 ,则“兵”位于点( )
 A、 B、 C、 D、4. 如图,在锐角 中, 分别是 边上的高, 交于点 , ,则 的度数是( )
A、 B、 C、 D、4. 如图,在锐角 中, 分别是 边上的高, 交于点 , ,则 的度数是( ) A、 B、 C、 D、5. 如图,要使AD//BC,那么可以选择下列条件中的 ( )
A、 B、 C、 D、5. 如图,要使AD//BC,那么可以选择下列条件中的 ( ) A、 B、 C、 D、6. 下列命题中的真命题是( )A、锐角大于它的余角 B、锐角大于它的补角 C、钝角大于它的补角 D、锐角与钝角之和等于平角7. 小林家今年1―5月份的用电量情况如图所示,由图可知,相邻的两个月中,用电量变化最大的是( )
A、 B、 C、 D、6. 下列命题中的真命题是( )A、锐角大于它的余角 B、锐角大于它的补角 C、钝角大于它的补角 D、锐角与钝角之和等于平角7. 小林家今年1―5月份的用电量情况如图所示,由图可知,相邻的两个月中,用电量变化最大的是( ) A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月8. 关于 的不等式 的解集如图所示,则 的取值是( )
A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月8. 关于 的不等式 的解集如图所示,则 的取值是( ) A、-1 B、-2 C、-3 D、-4
A、-1 B、-2 C、-3 D、-4二、填空题
-
9. |3﹣π|的计算结果是 .10. 2019年是中华人民共和国成立70周年,天安门广场举行了盛大的国庆阅兵式和群众游行活动.其中,群众游行队伍以“同心共筑中国梦”为主题,包含有“建国创业”“改革开放”“伟大复兴”三个部分,某同学要统计本班学生最喜欢哪个部分,制作扇形统计图.以下是打乱了的统计步骤:
①绘制扇形统计图
②收集三个部分本班学生喜欢的人数
③计算扇形统计图中三个部分所占的百分比
其中正确的统计顺序是 .
11. 如图,AB∥CD,∠B=160°,∠D=120°,则∠E= 12. 若M(4,2),点N(4,5),则直线 与轴平行.13. 在一个 边形中,除了一个内角外,其余的内角的和是 ,那么这个未知角是 度,这个多边形的边数是 .14. 已知三条不同的直线a,b,c在同一平面内,如果 , ,那么 ,这是一个命题.(填“真”或“假”)15. 如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2 , 则△BDE的面积为.
12. 若M(4,2),点N(4,5),则直线 与轴平行.13. 在一个 边形中,除了一个内角外,其余的内角的和是 ,那么这个未知角是 度,这个多边形的边数是 .14. 已知三条不同的直线a,b,c在同一平面内,如果 , ,那么 ,这是一个命题.(填“真”或“假”)15. 如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2 , 则△BDE的面积为.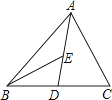 16. 点 到 轴, 轴的距离分别是 , ,则点 的坐标可能是 .
16. 点 到 轴, 轴的距离分别是 , ,则点 的坐标可能是 .三、解答题
-
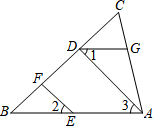
17. 解不等式组 .18. 如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD的度数.
 19. 已知点 ,
19. 已知点 , (1)、在坐标系中描出各点,先画出 、再把 先向左平移4个单位长度,再向下平移3个单位长度得到 ,请在图上画出 ;(2)、求 的面积;(3)、设点P在x轴上,且 与 的面积相等,求点P的坐标.20. 在抗击新冠疫情期间,市教委组织开展了“停课不停学”的活动.为了解此项活动的开展情况,市教委督导部门准备采用以下调查方式中的一种进行调查:
(1)、在坐标系中描出各点,先画出 、再把 先向左平移4个单位长度,再向下平移3个单位长度得到 ,请在图上画出 ;(2)、求 的面积;(3)、设点P在x轴上,且 与 的面积相等,求点P的坐标.20. 在抗击新冠疫情期间,市教委组织开展了“停课不停学”的活动.为了解此项活动的开展情况,市教委督导部门准备采用以下调查方式中的一种进行调查:A.从某所普通中学校随机选取200名学生作为调查对象进行调查;
B.从市内某区的不同学校中随机选取200名学生作为调查对象进行调查;
C.从市教育部门学生学籍档案中随机抽取200名学生作为调查对象进行调查.
 (1)、在上述调查方式中,你认为比较合理的一个是(填番号).(2)、如图,是按照一种比较合理的调查方式所得到的数据制成的频数分布直方图,在这个调查中,所抽取200名学生每天“停课不停学”的学习时间在1~2小时之间的人数m=.(3)、已知全市共有100万学生,请你利用(2)问中的调查结果,估计全市每天“停课不停学”的学习时间在1~2小时及以上的人数有多少?(4)、你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.21. 点C为直线AB上一点,点M.N分别是线段AC.线段BC的中点.
(1)、在上述调查方式中,你认为比较合理的一个是(填番号).(2)、如图,是按照一种比较合理的调查方式所得到的数据制成的频数分布直方图,在这个调查中,所抽取200名学生每天“停课不停学”的学习时间在1~2小时之间的人数m=.(3)、已知全市共有100万学生,请你利用(2)问中的调查结果,估计全市每天“停课不停学”的学习时间在1~2小时及以上的人数有多少?(4)、你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.21. 点C为直线AB上一点,点M.N分别是线段AC.线段BC的中点. (1)、如图,若C为线段AB上一点, , ,求线段MN的长;(2)、若C为线段AB上任一点,满足 ,其他条件不变,请直接写出线段MN的长(用含a的代数式表示);(3)、若C为线段AB的延长线上一点,且满足 ,其他条件不变,请画出图形并求出线段MN的长(用含b的代数式表示).
(1)、如图,若C为线段AB上一点, , ,求线段MN的长;(2)、若C为线段AB上任一点,满足 ,其他条件不变,请直接写出线段MN的长(用含a的代数式表示);(3)、若C为线段AB的延长线上一点,且满足 ,其他条件不变,请画出图形并求出线段MN的长(用含b的代数式表示).

