北京市通州区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-07-20 类型:期末考试
一、单选题
-
1. 在式子-3<0,x≥2,x=a,x2-2x,x≠3,x+1>y中,是不等式的有( )A、2个 B、3个 C、4个 D、5个2. 下列计算正确的是( )A、x+x2=x3 B、x2•x3=x6 C、x9÷x3=x3 D、(x3)2=x63. 如果 ,那么 的值为( )A、-1 B、1 C、-3 D、34. 北京春夏之季鲜花烂漫,空气中弥漫着各种花粉,有一种花粉的直径是0.000063米,将0.000063用科学记数法表示应为( )A、6.3×10﹣4 B、0.63×10﹣4 C、6.3×10﹣5 D、63×10﹣55. 如图,直线AB,CD被直线EF所截,交点分别为点E,F,若AB∥CD,下列结论正确的是( )
 A、∠1=∠3 B、∠2=∠4 C、∠2=∠5 D、∠4=∠56. 小颖随机抽样调查本校20名女同学所穿运动鞋尺码,并统计如表:
A、∠1=∠3 B、∠2=∠4 C、∠2=∠5 D、∠4=∠56. 小颖随机抽样调查本校20名女同学所穿运动鞋尺码,并统计如表:尺码/cm
21.5
22.0
22.5
23.0
23.5
人数
2
4
3
8
3
学校附近的商店经理根据统计表决定本月多进尺码为23.0cm的女式运动鞋,商店经理的这一决定应用的统计量是( )
A、平均数 B、加权平均数 C、众数 D、中位数7. 下列因式分解正确的是( )A、 B、 C、 D、8. 如图,将三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )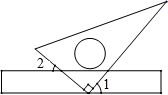 A、30° B、40° C、50° D、60°9. 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
A、30° B、40° C、50° D、60°9. 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )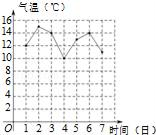 A、13,13 B、14,14 C、13,14 D、14,1310. 《九章算术》是我国东汉初年编订的一部数学经典著作在它的“方程”一章里,一次方程组是由算筹布置而成的《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2图中各行从左到右列出的算筹数分别表示未知数 的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 类似地,图2所示的算筹图我们可以表述为( )
A、13,13 B、14,14 C、13,14 D、14,1310. 《九章算术》是我国东汉初年编订的一部数学经典著作在它的“方程”一章里,一次方程组是由算筹布置而成的《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2图中各行从左到右列出的算筹数分别表示未知数 的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 类似地,图2所示的算筹图我们可以表述为( )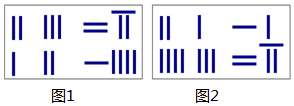 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:x2y﹣6xy+9y= .12. 化简(x+y)2+(x+y)(x-y)=.13. 将一副三角板如图摆放,若∠BAC=31°45′,则∠EAD的度数是 .
 14. 北京市今年5月份最后六天的最高气温分别为31,34,36,27,25,33(单位:℃). 这组数据的中位数是15. 在实数范围内定义一种新运算“⊕”,其运算规则为:a⊕b=2a+3b.如:1⊕5=2×1+3×5=17.则不等式x⊕4<0的解集为 .16. 如图1,将边长为a的大正方形剪去一个边长为b的小正方形,并沿图中的虚线剪开,拼接后得到图2,请根据图形的面积写出一个含字母a,b的等式.
14. 北京市今年5月份最后六天的最高气温分别为31,34,36,27,25,33(单位:℃). 这组数据的中位数是15. 在实数范围内定义一种新运算“⊕”,其运算规则为:a⊕b=2a+3b.如:1⊕5=2×1+3×5=17.则不等式x⊕4<0的解集为 .16. 如图1,将边长为a的大正方形剪去一个边长为b的小正方形,并沿图中的虚线剪开,拼接后得到图2,请根据图形的面积写出一个含字母a,b的等式.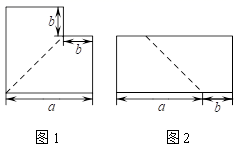 17. 如图,把一张长方形纸片沿AB折叠,已知∠1=75°,则∠2的度数为 .
17. 如图,把一张长方形纸片沿AB折叠,已知∠1=75°,则∠2的度数为 . 18. 在① ② ③ 中,①和②是方程 的解;是方程 的解;不解方程组,可写出方程组 的解为 .
18. 在① ② ③ 中,①和②是方程 的解;是方程 的解;不解方程组,可写出方程组 的解为 .三、解答题
-
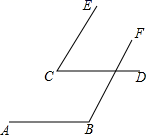
19. 计算:(﹣1)2021+(3.14﹣π)0+2﹣1 .20. 分解因式: .21. 用代入法解方程组22. 解不等式 > ﹣1,并写出它的非负整数解.23. 已知关于x,y的二元一次方程组 的解为 求 的值.24. 已知:如图,AB//CD , CE//BF . 求证:∠C+∠B=180°.
 25. 某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题:
25. 某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题: (1)、本次共调查了多少名学生?(2)、请将两个统计图补充完整.(3)、若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?
(1)、本次共调查了多少名学生?(2)、请将两个统计图补充完整.(3)、若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?
26. 某公园对一个边长为a(a>1)的正方形花坛进行改造,由于占地需要,正方形花坛南北方向需要缩短1米,使其形状成为长方形.为了使花坛中的绿植面积不变,公园决定将花坛向东侧扩展,使得到的长方形面积和原来正方形的面积相等.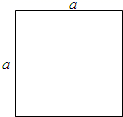 (1)、小明说:这太简单了,把正方形南北方向减少1米,在花坛东侧增加1米就行了.这样得到的长方形的周长和面积与原来正方形的周长和面积都相等.你认为小明说的对吗?请你说明理由.(2)、如果原来正方形的花坛边长是5米,在只保证面积不变的情况下,请你计算出改造后,向东扩展了多少米?(3)、如果正方形的花坛边长是a米,在只保证面积不变的情况下,请你用代数式表示出改造后长方形的长.27. 已知:如图,点C在 的一边OA上,过点C的直线 ,CF平分 , 于C.
(1)、小明说:这太简单了,把正方形南北方向减少1米,在花坛东侧增加1米就行了.这样得到的长方形的周长和面积与原来正方形的周长和面积都相等.你认为小明说的对吗?请你说明理由.(2)、如果原来正方形的花坛边长是5米,在只保证面积不变的情况下,请你计算出改造后,向东扩展了多少米?(3)、如果正方形的花坛边长是a米,在只保证面积不变的情况下,请你用代数式表示出改造后长方形的长.27. 已知:如图,点C在 的一边OA上,过点C的直线 ,CF平分 , 于C.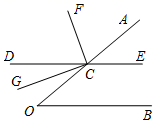 (1)、若 ,求 的度数;(2)、求证:CG平分 ;(3)、当 为多少度时,CD平分 ,并说明理由.28.(1)、问题情境:如图1,AB//CD , ∠PAB=130°,∠PCD=120°.求∠APC度数.
(1)、若 ,求 的度数;(2)、求证:CG平分 ;(3)、当 为多少度时,CD平分 ,并说明理由.28.(1)、问题情境:如图1,AB//CD , ∠PAB=130°,∠PCD=120°.求∠APC度数.小明的思路是:如图2,过P作PE∥AB , 通过平行线性质,可得∠APC= .
(2)、问题迁移:如图3,AD//BC , 点P在射线OM上运动,∠ADP=∠α , ∠BCP=∠β .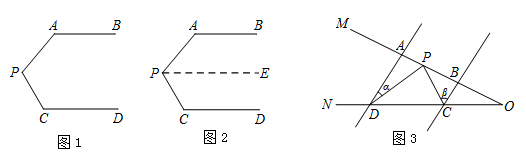
当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(3)、如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.