北京市怀柔区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-07-20 类型:期末考试
一、单选题
-
1. (-a5)2+(-a2)5的结果是( )A、0 B、 C、 D、2. 如图:点C是直线AB上一点,过点C作CD⊥CE,那么图中 和 的关系是( ).
 A、互补 B、互余 C、对顶角 D、同位角3. 不等式2x﹣3>1的解集在数轴上表示正确的是( )A、
A、互补 B、互余 C、对顶角 D、同位角3. 不等式2x﹣3>1的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、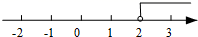 D、
D、 4. 已知 是方程 的一个解,那么a的值为( )A、-3 B、-1 C、1 D、35.
4. 已知 是方程 的一个解,那么a的值为( )A、-3 B、-1 C、1 D、35.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=35°,那么∠B的度数为( )
 A、35° B、45° C、55° D、145°6. 某健步走运动爱好者用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )
A、35° B、45° C、55° D、145°6. 某健步走运动爱好者用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( ) A、1.2,1.3 B、1.3,1.3 C、1.4,1.35 D、1.4,1.37. 鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )
A、1.2,1.3 B、1.3,1.3 C、1.4,1.35 D、1.4,1.37. 鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( ) A、鸡 20 只,兔 15 只 B、鸡 12 只,兔 23 只 C、鸡 15 只,兔 20 只 D、鸡 23 只,兔 12 只8. 将 3a2m﹣6amn+3a分解因式,下面是四位同学分解的结果:①3am(a﹣2n+1);②3a(am+2mn﹣1);③3a(am﹣2mn);④3a(am﹣2mn+1).其中,正确的是( )A、① B、② C、③ D、④9. 某市居民用电的电价实行阶梯收费,收费标准如下表:
A、鸡 20 只,兔 15 只 B、鸡 12 只,兔 23 只 C、鸡 15 只,兔 20 只 D、鸡 23 只,兔 12 只8. 将 3a2m﹣6amn+3a分解因式,下面是四位同学分解的结果:①3am(a﹣2n+1);②3a(am+2mn﹣1);③3a(am﹣2mn);④3a(am﹣2mn+1).其中,正确的是( )A、① B、② C、③ D、④9. 某市居民用电的电价实行阶梯收费,收费标准如下表:一户居民每月用电量x(度)
电费价格(元/度)
0.48
0.53
0.78
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,则李叔家七月份最多可用电的度数是( ).
A、100 B、400 C、396 D、39710. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( ) A、2a﹣3b B、4a﹣8b C、2a﹣4b D、4a﹣10b
A、2a﹣3b B、4a﹣8b C、2a﹣4b D、4a﹣10b二、填空题
-
11. 分解因式:3a2﹣6a+3= .12. 若a+b=5,ab=6,则a2+b2= .13. 图是根据某校为地震灾区捐款的情况而制作的统计图,已知该校在校学生有600人,请根据统计图计算该校共捐款元.
 14. 已知,如图,要使得AB∥CD,你认为应该添加的一个条件是
14. 已知,如图,要使得AB∥CD,你认为应该添加的一个条件是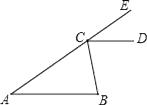 15. 写出不等式组 的整数解为.16. 如图,直线AB、CD、EF相交于点O , AB⊥CD , OG平分∠AOE , 如果∠FOD = 28°,那么∠AOG =度.
15. 写出不等式组 的整数解为.16. 如图,直线AB、CD、EF相交于点O , AB⊥CD , OG平分∠AOE , 如果∠FOD = 28°,那么∠AOG =度. 17. 已知x,y是有理数,且 ,则18. 将边长为1的正方形纸片按如图所示方法进行对折,第1次对折后得到的图形面积为S1 , 第2次对折后得到的图形面积为S2 , …,第n次对折后得到的图形面积为Sn , 则S4= , S1+S2+S3+…+S2021= .
17. 已知x,y是有理数,且 ,则18. 将边长为1的正方形纸片按如图所示方法进行对折,第1次对折后得到的图形面积为S1 , 第2次对折后得到的图形面积为S2 , …,第n次对折后得到的图形面积为Sn , 则S4= , S1+S2+S3+…+S2021= . 19. 如图,已知CD⊥DA , DA⊥AB , ∠1=∠2.试说明DF∥AE . 请你完成下列填空,把证明过程补充完整.
19. 如图,已知CD⊥DA , DA⊥AB , ∠1=∠2.试说明DF∥AE . 请你完成下列填空,把证明过程补充完整.
证明:∵ ▲ ,
∴∠CDA=90°,∠DAB=90° ( ▲ ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ▲ ( ▲ ),
∴DF∥AE ( ▲ ).
三、解答题
-
20. 计算:(1)、(π﹣2021)0﹣(﹣ )﹣2+(﹣3)2(2)、(2x2)3•(﹣4y3)÷(4xy)221. 解不等式 +1≤3,并把解集在数轴上表示出来.
 22. 因式分解:(1)、 ;(2)、 .23. 解方程组 .24. 已知: ,求代数式 的值.25. 某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
22. 因式分解:(1)、 ;(2)、 .23. 解方程组 .24. 已知: ,求代数式 的值.25. 某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.表1:小张抽样调查单位3名职工的健康指数
年龄
26
42
57
健康指数
97
79
72
表2:小王抽样调查单位10名职工的健康指数
年龄
23
25
26
32
33
37
39
42
48
52
健康指数
93
89
90
83
79
75
80
69
68
60
表3:小李抽样调查单位10名职工的健康指数
年龄
22
29
31
36
39
40
43
46
51
55
健康指数
94
90
88
85
82
78
72
76
62
60
根据上述材料回答问题:
(1)、扇形统计图中老年职工所占部分的圆心角度数为(2)、小张、小王和小李三人中,的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处 . 26. 已知关于x,y的方程组 的x,y的值之和等于2,求m的值.27. 如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
26. 已知关于x,y的方程组 的x,y的值之和等于2,求m的值.27. 如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD. 28. 为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
28. 为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:A型
B型
价格(万元/台)
a
b
年载客量(万人/年)
60
100
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)、求a,b的值;
(2)、如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
29. 探究题:学习完平行线的性质与判定之后,我们发现借助构造平行线的方法可以帮我们解决许多问题.(1)、小明遇到了下面的问题:如图1,l1∥l2 , 点P在l1、l2内部,探究∠A , ∠APB , ∠B的关系.小明过点P作l1的平行线,可证∠APB , ∠A , ∠B之间的数量关系是:∠APB= .(2)、如图2,若AC∥BD , 点P在AC、BD外部,∠A , ∠B , ∠APB的数量关系是否发生变化?请你补全下面的证明过程.过点P作PE∥AC .
∴∠A= ▲
∵AC∥BD
∴ ▲ ∥ ▲
∴∠B= ▲
∵∠BPA=∠BPE﹣∠EPA
∴ ▲ .
(3)、随着以后的学习你还会发现平行线的许多用途,试构造平行线解决以下问题:已知:如图3,三角形ABC , 求证:∠A+∠B+∠C=180°.