北京市房山区燕山地区2020-2021学年七年级下学期数学期末试卷
试卷更新日期：2021-07-20 类型：期末考试
一、单选题
-
1. 北京2022年冬奥会会徽是以汉字“冬”为灵感来源设计的（如图）．下面四个图案中，可以通过平移图案得到的是（ ）
A、
B、
C、
D、
2. 9的平方根是（ ）A、3 B、 C、±3 D、3. 在平面直角坐标系中，下列各点位于第四象限的是( )A、(－2，3) B、(2，3) C、(2，－3) D、(－2，－3)4. 下列调查中，不适合采用全面调查（普查）方式的是（ ）A、调查新冠疫情期间乘坐地铁的乘客体温情况 B、调查“祝融号火星车”零部件质量状况 C、调查本校七年级（1）班学生观看电影《我和我的家乡》情况 D、调查国产纯电动汽车蓄电池的续航里程情况5. 如图，从人行横道线上的点P处过马路，沿线路PB行走距离最短，其依据的几何学原理是（ ）
A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、在同一平面内，过一点有且只有一条直线与已知直线垂直6. 已知 ，则下列结论正确的是（ ）A、 B、 C、 D、7. 如图，直线a，b被c，d所截，∠1＋∠2＝180°，∠3＝60°，则∠4的度数为（ ）
A、30° B、45° C、60° D、120°8. 如图是老北京城一些地点的分布示意图，在图中，分别以正东，正北方向为 轴， 轴的正方向建立平面直角坐标系．如果表示东直门的点的坐标为（3.5，4），表示宣武门的点的坐标为（－2，－1），那么坐标原点所在的位置是（ ）
A、天安门 B、正阳门 C、西直门 D、阜成门9. 我们定义一个关于实数a，b的新运算，规定：a*b＝3a－2b，例如，4*5＝3×4－2×5，若实数m满足m*2＜1，则m的取值范围是（ ）A、 B、 C、 D、10. 我国是一个水资源严重短缺的国家，本世纪以来，我国政府相继采取了南水北调、推进海绵城市建设、水资源循环利用等一系列措施来缓解水资源匮乏对经济社会发展的制约．下面是根据国家统计局发布的有关信息绘制的统计图．2014~2019年全国生活用水总量统计图
2019年全国用水结构统计图
根据统计图提供的信息，下列推断不合理的是（ ）
A、2014－2019年，全国生活用水总量逐年增加 B、2014－2019年，全国用水总量大约每年增长2% C、2019年，全国农业用水总量约为工业用水总量的3倍 D、2019年，全国用水总量约为6020亿立方米二、填空题
-
11. 写出一个比－3小的无理数 ．12. x的5倍与3的和是非负数，用不等式表示为 ．13. 点A（m，5）到x轴和y轴的距离相等，则点A的坐标为 ．14. 已知 是方程为 的解，则m的值为 ．15. 如图，AB⊥AC，∠1＝30°，要使AD∥BC，需再添加的一个条件为： ．
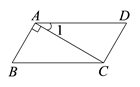16. 关于 的不等式 的解集为 ，请写出一组满足条件的实数a，b的值：a＝ ，b＝ ．17. 在“互联网＋”时代，国家积极推动信息化技术与传统教学方式的深度融合，实现线上、线下融合式教学模式变革．为了解本校学生对融合式教学模式的喜爱程度，李校长对全校学生进行了问卷调查，并对调查结果按“非常喜欢”，“喜欢”，“一般”，“不喜欢”四个等级进行统计，以下是排乱的统计步骤：A.从扇形图中分析出学生对融合式教学模式的喜爱程度
B.发放调查问卷，并利用问卷星收集学生问卷数据
C.绘制扇形图来表示各等级所占的百分比
D.整理所收集的数据并绘制频数分布表
正确的统计步骤的顺序是 ． （用字母按顺序写出即可）
18. 我们知道“对于实数m，n，k，若m＝n，n＝k，则m＝k”，即相等关系具有传递性．小捷由此进行联想，提出了下列命题：①对于实数a，b，c，若a＞b，b＞c，则a＞c；
②对于直线a，b，c，若a⊥b，b⊥c，则a⊥c；
③对于角α，β，γ，若α与β互为邻补角，β与γ互为邻补角，则α与γ互为邻补角；
④对于图形M，N，P，若M可以平移到N，N可以平移到P，则M可以平移到P．
其中所有真命题的序号是 ．
三、解答题
-
19. 计算： ．20. 解不等式 ，并写出它的所有正整数解．21. 解方程组：22. 解不等式组： ，并把它的解集在数轴上表示出来．
23. 如图，AD⊥BC，垂足为D，EF⊥BC，垂足为点F，∠E＝∠3，求证：AD是∠BAC的平分线．请将下面的证明过程补充完整．
证明：∵AD⊥BC，EF⊥BC，（已知）
∴∠4＝∠5＝90°，（垂直定义）
∴AD//EF，（ ）
∴∠E＝∠2，（ 两直线平行，同位角相等 ）
∠3＝ ▲ ．（ ）
∵ ▲ ， （已知）
∴ ▲ ， （等量代换）
∴AD是∠BAC的平分线．（角平分线定义）
24. 每年的4月23日是联合国教科文组织确定的“世界读书日”，又称“世界图书和版权日”．红星中学在“世界读书日”开展“弘扬传统文化，阅读经典名著”主题活动，计划购置一批书籍．已知每本《诗经》25元，每本《论语》18元，该学校决定购买《诗经》和《论语》共100本，总费用不超过2000元，那么该学校最多可以购买《诗经》多少本？25. 为庆祝中国共产党建党100周年，使学生进一步了解中国共产党的历史，某学校组织了“党史百年天天读”活动，并进行了一次全校2000名学生都参加的书面测试，阅卷后，教学处随机抽取了100份答卷进行分析统计，发现考试成绩x（分）的最低分为50分，最高分为满分100分，且分数都为整数，并绘制了尚不完整的统计图表：分数段（x分）
频数
频率
50≤x＜60
4
0.04
60≤x＜70
a
0.20
70≤x＜80
30
0.30
80≤x＜90
26
b
90≤x＜100
15
0.15
100≤x＜110
5
0.05
请根据统计图表提供的信息，解答下列问题：
(1)、在频数分布表中，a＝ ；b＝ ；(2)、请将频数分布直方图补充完整，并在图中标明相应数据；(3)、该校对成绩为90≤x≤100的学生进行奖励，按成绩从高分到低分设一，二，三等奖，各奖项的人数占比如扇形统计图所示．① 在扇形图中，二等奖所在扇形的圆心角度数为°；
② 请你估算全校获得一等奖的学生人数约为人．
26. 如图，AB∥CD，直线MN交AB于点E，交CD于点F，点P是直线MN上一个动点，过点P作PG⊥MN交CD于点G．
(1)、当点P运动到图1位置时，① 依题意补全图1；
② 判断∠PGD与∠AEM的数量关系，并说明理由；
(2)、当点P运动到图2位置时，直接用等式表示出∠PGD与∠AEM的数量关系．（不需要证明）27. 如图，在平面直角坐标系xOy中，点A（a－1，a＋2）位于第一象限，将点A向下平移一定单位长度得到点B（1，0），以AB为边在AB右侧作正方形ABCD．
(1)、求a的值及点D的坐标；(2)、横、纵坐标都是整数的点叫做整点．已知点M（－5，0），N（0，5），将正方形ABCD向左平移m（m＞0）个单位长度，得到正方形A′B′C′D′，记正方形A′B′C′D′ 和△OMN重叠的区域（不含边界）为W．① 当m＝3时，区域W内的整点个数为；
② 若区域W内恰有3个整点，直接写出m的取值范围 ．