北京市东城区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个数中，无理数是（　　）

A、 $\frac{22}{7}$ B、 $0. \dot{5}$ C、 $\frac{π}{2}$ D、﹣ $\sqrt{36}$

查看试题解析
2. 下列调查方式中，适宜的是（　　）

A、合唱节前，某班为定制服装，对同学们的服装尺寸大小采用抽样调查 B、某大型食品厂为了解所生产的食品的合格率，采用全面调查 C、对乘坐某航班的乘客进行安检，采用全面调查 D、某市为了解该市中学生的睡眠情况，选取某中学初三年级的学生进行抽样调查

查看试题解析
3. 如图，把小河里的水引到田地A处，若使水沟最短，则过点A向河岸l作垂线，垂足为点B，沿AB挖水沟即可，理由是（　　）

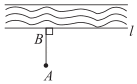A、两点之间，线段最短 B、垂线段最短 C、两点确定一条直线 D、过一点可以作无数条直线

查看试题解析
4. 如图，点A，C，E在同一条直线上，下列条件中能判断AB∥CD的是（　　）

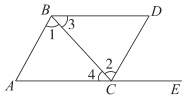A、∠1＝∠4 B、∠3＝∠4 C、∠1＝∠2 D、∠D+∠ACD＝180°

查看试题解析
5. 已知点 $P (m + 2 ， 2 m ﹣ 4)$ 在 $x$ 轴上，则点 $P$ 的坐标是（）

A、 $(4 ， 0)$ B、 $(0 ， 4)$ C、 $(- 4 ， 0)$ D、 $(0, - 4)$

查看试题解析
6. 如果a＜b，那么下列不等式中错误的是（　　）

A、a+2＜b+2 B、a﹣2＜b﹣2 C、 $\frac{a}{2} < \frac{b}{2}$ D、﹣2a＜﹣2b

查看试题解析
7. 如图，直线a $//$ b，点B在a上，且AB⊥BC．若∠1＝35°，则∠2等于（　　）

A、35° B、50 C、55° D、65°

查看试题解析
8. 如图，数轴上有A，B，C，D四点，以下线段中，长度最接近 $\sqrt{10}$ 的是（　　）

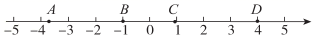A、线段AB B、线段AC C、线段BC D、线段CD

查看试题解析
9. 我国古代数学著作《九章算术》“盈不足”一章中记载：“今有大器五小器一容三斛，大器一小器五容二斛，问大小器各容几何”.意思是：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛，1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛？设1个大桶盛酒x斛，1个小桶盛酒y斛，下列方程组正确的是（）.

A、 ${\begin{array}{l} 5 x + y = 3 \\ x + 5 y = 2 \end{array}$ B、 ${\begin{array}{l} 5 x + y = 2 \\ x + 5 y = 3 \end{array}$ C、 ${\begin{array}{l} 5 x + 3 y = 1 \\ x + 2 y = 5 \end{array}$ D、 ${\begin{array}{l} 3 x + y = 5 \\ 2 x + 5 y = 1 \end{array}$

查看试题解析
10. 如图，在平面直角坐标系xOy中，已知点A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2）．现把一条长为2021个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A→B→C→D→A→B……的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（　　）

A、（1，1） B、（0，1） C、（﹣1，1） D、（1，0）

查看试题解析

二、填空题

11. “两条直线被第三条直线所截，内错角相等”是命题．（填“真”或“假”）

查看试题解析
12. “x的2倍与y的和是非负数”用不等式表示应为．

查看试题解析
13. 若关于x，y的二元一次方程组 ${\begin{array}{l} x + y = 2 ① \\ A = 0 ② \end{array}$ 的解为 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ ，则方程②可以是．（写出一个即可）

查看试题解析
14. 如图，直线AB与CD相交于点O，OE⊥CD．若∠EOB＝2∠AOC，则∠AOD的度数为．

查看试题解析
15. 下面是某市2013~2016年私人汽车拥有量和年增长率的统计图，该市私人汽车拥有量年净增量最多的是年，私人汽车拥有量年增长率最大的是年．

查看试题解析
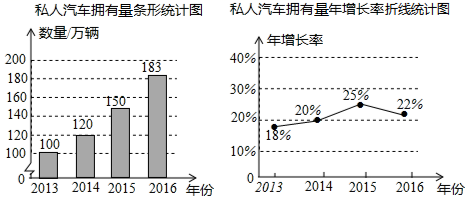16. 在平面直角坐标系xOy中，已知点A（a，﹣1），B（2，3﹣b），C（﹣5，4）．若AB∥x轴，AC∥y轴，则a+b＝．

查看试题解析
17. 如果一元一次方程的解也是一元一次不等式组的解，那么称该一元一次方程为该不等式组的关联方程．例如：方程x﹣3＝0的解为x＝3，不等式组 ${\begin{array}{l} x - 1 > 0 \\ x < 4 \end{array}$ 的解集为1＜x＜4，因为1＜3＜4，所以方程x﹣3＝0为不等式组 ${\begin{array}{l} x - 1 > 0 \\ x < 4 \end{array}$ 的关联方程．若方程2x+1＝x+2与3（x﹣1）＝x+1都是关于x的不等式组 ${\begin{array}{l} x - 6 < m \\ 2 x \geq x + m \end{array}$ 的关联方程，则满足题意的整数m可以是（写出一个即可）；m的取值范围是．

查看试题解析

三、解答题

18. 计算： $\sqrt{{(- 4)}^{2}} - \sqrt[3]{27} + | - \sqrt{2} |$ ．

查看试题解析
19. 解不等式3（x﹣1）≥x+2，并将解集表示在数轴上．

查看试题解析
20. 解不等式组 ${\begin{array}{l} 4 x - 3 \geq x - 10 \\ \frac{2 x + 5}{3} - 1 < 4 - x \end{array}$ 并写出所有整数解．

查看试题解析
21. 如图，平面内有两条直线l₁ ， l₂点A在直线l₁上，按要求画图并填空：

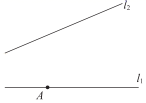(1)、若AB＝12，AC＝13，则点A到直线l₂的距离等于．

(2)、①过点A画l₂的垂线段AB，垂足为点B；

②6过点A画直线AC⊥l₁ ，交直线l₂于点C；

③过点A画直线AD∥l₂；

查看试题解析
22. 按要求画图并填空：
在由边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系xOy，原点O及△ABC的顶点都是格点（横、纵坐标都是整数的点称为格点），点A的坐标为（﹣4，2）．

(1)、将△ABC先向下平移1个单位长度，再向右平移4个单位长度得到△A₁B₁C₁ ，画出△A₁B₁C₁；

(2)、点A₁的坐标是；

(3)、点D在x轴正半轴上，若S_△ABD＝S_△ABC ，则点D的坐标为．

查看试题解析
23. 补全证明过程，并在（　　）内填写推理的依据．
已知：如图，直线a，b，c被直线d，e所截，∠1＝∠2，∠4+∠5＝180°，求证：∠6＝∠7．

证明：∵∠1＝∠2，∠2＝∠3（     ），

∴∠1＝∠3，

∴c∥a（     ），

∵∠4+∠5＝180°，

∴　▲　∥b（（     ）．

∴a∥b（     ）．

∴∠6＝∠7（     ）．

查看试题解析
24. 如图，在三角形ABC中，点D，E分别在AB，AC上，点F，G在BC上，EF与DG交于点O，∠1+∠2＝180°，∠B＝∠3．

(1)、判断DE与BC的位置关系，并证明；

(2)、若∠C＝63°，求∠DEC的度数．

查看试题解析
25. 为了解某校学生在五一假期阅读的情况，随机抽取了若干名学生进行调查，获得他们的阅读时间（单位：h），并对数据（时间）进行整理、描述．下面给出了部分信息：图1是阅读时间频数分布直方图（数据分成5组：2≤t＜4，4≤t＜6，6≤t＜8，8≤t＜10，10≤t≤12），图2是阅读时间扇形统计图．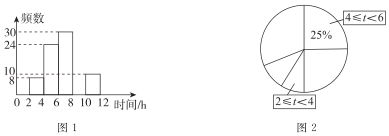

根据以上信息，回答下列问题：

(1)、本次调查的样本容量是；

(2)、补全图1；

(3)、图2中，2≤t＜4所在的扇形的圆心角的度数是；

(4)、已知该校共有1800名学生，估计该校学生在五一假期阅读时间不少于6h的人数．

查看试题解析
26. 小勇到某文具店为班级购买奖品．该文具店举办“文具组合”促销活动，具体如下：

A组合：一个笔袋、一支签字笔单价a元

B组合：一个笔袋、一副三角板单价b元

C组合：一个笔袋、一支签字笔、一副三角板单价33元

已知B组合的单价比A组合的单价多3元，2份A组合和1份B组合共需78元．请回答以下问题：

(1)、A，B组合的单价分别是多少元？

(2)、若他共购买了8个笔袋、5支签字笔、n副三角板，则他选了份A组合份B组合、份C组合；（可用含n的代数式表示）

(3)、在（2）的条件下，如果三种组合至少各买1份，而且总费用不超过240元，那么小勇有多少种购买方案，哪种方案总费用最低？

查看试题解析
27. 在平面直角坐标系xOy中．点A，B，P不在同一条直线上．对于点P和线段AB给出如下定义：过点P向线段AB所在直线作垂线，若垂足Q落在线段AB上，则称点P为线段AB的内垂点．若垂足Q满足|AQ-BQ|最小，则称点P为线段AB的最佳内垂点．已知点A（﹣2，1），B（1，1），C（﹣4，3）．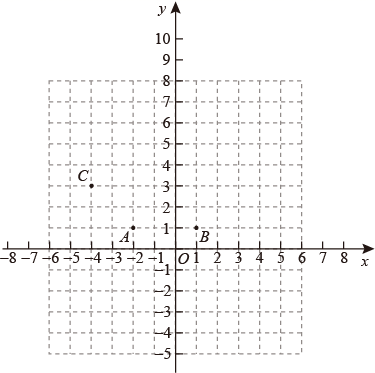

(1)、在点P₁（2，3）、P₂（﹣5，0）、P₃（﹣1，﹣2），P₄（﹣ $\frac{1}{2}$ ，4）中，线段AB的内垂点为；

(2)、点M是线段AB的最佳内垂点且到线段AB的距离是2，则点M的坐标为；

(3)、点N在y轴上且为线段AC的内垂点，则点N的纵坐标n的取值范围是；

(4)、已知点D（m，0），E（m+4，0），F（2m，3）．若线段CF上存在线段DE的最佳内垂点，求m的取值范围．

查看试题解析