天津市南开区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，点P是平面坐标系中一点，则点P到原点的距离是（）

A、3 B、 $\sqrt{2}$ C、 $\sqrt{7}$ D、 $\sqrt{53}$

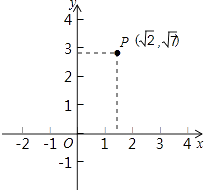查看试题解析
2. 若关于x的一元二次方程 $(a - 2) x^{2} + 2 x + a^{2} - 4 = 0$ 有一个根为0，则a的值为（）

A、 $\pm 2$ B、 $\pm \sqrt{2}$ C、-2 D、2

查看试题解析
3. 在庆祝新中国成立70周年的校园歌唱比赛中，11名参赛同学的成绩各不相同，按照成绩取前5名进入决赛．如果小明知道了自己的比赛成绩，要判断能否进入决赛，小明需要知道这11名同学成绩的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 下列一元二次方程中，没有实数根的是（）

A、 $x^{2} + 2 x + 1 = 0$ B、 $x^{2} + x + 2 = 0$ C、 $x^{2} - 2 x = 0$ D、 ${(x - 3)}^{2} - 2 = 0$

查看试题解析
5. 满足下列条件的三角形中，是直角三角形的是（　　）

A、三个内角度数之比是3：4：5 B、三边长的平方比为5：12：13 C、三边长度是1： $\sqrt{2}$ ： $\sqrt{3}$ D、三个内角度数比为2：3：4

查看试题解析
6. 如图，在四边形 $A B C D$ 中，对角线 $A C$ 和 $B D$ 相交于点O ，下列条件在不能判断四边形 $A B C D$ 是平行四边形的是（）

A、 $A B / / D C ， A D / / B C$ B、 $A B = D C ， A D = B C$ C、 $O A = O C ， O B = O D$ D、 $A B / / D C ， A D = B C$

查看试题解析
7. 一次函数 $y = 2 x + 1$ 的图象过点 $(a - 1 ， y_{1}) ， (a ， y_{2}) ， (a + 1 ， y_{3})$ 则（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
8. 在平面直角坐标系中，将函数 $y = - 2 x$ 的图象向上平移4个单位长度，则平移后的图象与x轴交点的坐标为（）

A、 $(4 ， 0)$ B、 $(- 2 ， 0)$ C、 $(2 ， 0)$ D、 $(- 4 ， 0)$

查看试题解析
9. 已知菱形ABCD中，对角线AC与BD交于点O，∠BAD＝120°，AC＝4，则该菱形的面积是（）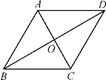

A、16 $\sqrt{3}$ B、16 C、8 $\sqrt{3}$ D、8

查看试题解析
10. 若某一样本的方差为 $s^{2} = \frac{1}{5} [{(5 - 7)}^{2} + {(7 - 7)}^{2} + {(8 - 7)}^{2} + {(x - 7)}^{2} + {(y - 7)}^{2}]$ ，样本容量为5．则下列说法：①当 $x = 9$ 时， $y = 6$ ；②该样本的平均数为7；③ $x$ ， $y$ 的平均数是7；④该样本的方差与 $x$ ， $y$ 的值无关．其中错误的是（）

A、①② B、②④ C、①③ D、③④

查看试题解析
11. 某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10%，5月份的营业额达到633.6万元，若该商场3月份到5月份营业额的月平均增长率为x ，则下面列出的方程中正确的是（）

A、 $633 .6 {(1 + x)}^{2} = 400 (1 + 10 %)$ B、 $633 .6 {(1 + 2 x)}^{2} = 400 \times (1 + 10 %)$ C、 $400 \times (1+10 %) {(1+ 2 x)}^{2} = 633.6$ D、 $400 \times (1+10 %) {(1+ x)}^{2} = 633.6$

查看试题解析
12. 在全民健身越野赛中，甲乙两选手的行程y（千米）随时间（时）变化的图象（全程）如图所示．有下列说法：①前半小时甲选手的速度为8千米/时；②第1小时两人都跑了10千米；③甲比乙先到达终点；④甲选手的速度一直比乙慢．其中正确的说法有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 若一直角三角形两直角边长分别为6和8，则斜边长为．

查看试题解析
14. 甲、乙两人在相同条件下进行射击练习，每人10次射击成绩的平均值都是7环，方差分别为 $S_{甲}^{2} = 2.5$ ， $S_{乙}^{2} = 1.2$ ，则两人成绩比较稳定的是（填“甲”或“乙”）.

查看试题解析
15. 在同一平面直角坐标系中，函数y₁＝kx+b与y₂＝mx+n的图象如图所示，则关于x的不等式kx+b≥mx+n的解集为．

查看试题解析
16. 将方程 $3 x^{2} - 6 x - 8 = 0$ 配方为 $a {(x - h)}^{2} = k$ ，其结果是．

查看试题解析
17. 如图所示，四边形 $A B C D$ 是长方形，把 $△ A C D$ 沿 $A C$ 折叠到 $△ A C D^{'}$ ， $A D$ 与 $B C$ 交于点E ，若 $A D = 4 ， D C = 3$ ，则 $B E$ 的长为．

查看试题解析
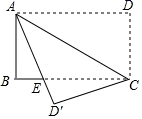18. 如图所示的网格是正方形网格，点A ， B ， C ， D ， E是网格线交点，则 $∠ B A C - ∠ D A E$ 的度数为．

查看试题解析

三、解答题

19. 解方程：
（Ⅰ） ${(x + 3)}^{2} = 36$

（Ⅱ） $3 x^{2} - 1 = 6 x$

查看试题解析
20. 某校为了解学生每周参加家务劳动的情况，随机调查了该校部分学生每周参加家务劳动的时间．根据调查结果，绘制出如图的统计图①和图②．请根据相关信息，解答下列问题：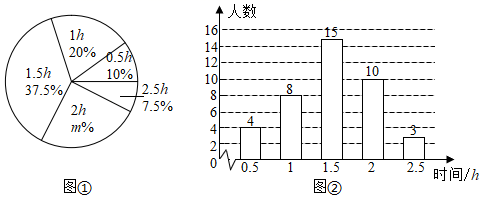

(1)、本次接受调查的学生人数为，图①中m的值为；

(2)、求统计的这组每周参加家务劳动时间数据的众数､中位数和平均数；

(3)、根据统计的这组每周参加家务劳动时间的样本数据，若该校共有800名学生，估计该校每周参加家务劳动的时间大于 $1 h$ 的学生人数．

查看试题解析
21. 如图，直线 $l_{1}$ 分别与x轴，y轴交于A､B两点，A､B的坐标分别为 $(2 ， 0)$ 、 $(0 ， 3)$ ，过点B的直线 $l_{2} ： y = \frac{1}{2} x + 3$ 交x轴于点C ，点 $D (n ， 6)$ 是直线l上的一点，连接 $C D$ ．

（Ⅰ）求 $l_{1}$ 的解析式；

（Ⅱ）求C､D的坐标；

（Ⅲ）求 $△ B C D$ 的面积．

查看试题解析
22. 在△ABC中，D为AC的中点，DM⊥AB于M，DN⊥BC于N，且DM=DN。

(1)、求证：△ADM≌△CDN

(2)、若AM=2，AB=AC，求四边形DMBN的周长。

查看试题解析

23. 某书店购一批故事书进行销售，其进价为每本40元，如果按每本故事书50元进行出售，每月可以售出500本故事书，后来经过市场调查发现，若每本故事书每涨价1元，则故事书的销量每月则减少20本，设每本故事书涨价x元

(x > 0)

．

(1)、根据题意填表：

每本故事书涨价（元）	1	2	…	x
每本故事书所获利润（元）	11	12	…
故事书每月的销量（本）	480		…

(2)、该书店要保证每月销售此种故事书盈利6000元，同时又要使购书者得到实惠，则每本故事书需涨价多少元?

(3)、若使该故事书的月销量不低于300本，则每本故事书的售价应不高于元．

查看试题解析

24. 如图，在正方形 $O A B C$ 中，边 $O A$ 、 $O C$ 分别在 $x$ 轴、 $y$ 轴上，点 $B$ 的坐标为 $(4 ， 4)$ ，点 $D$ 在线段 $O A$ 上，以点 $D$ 为直角顶点， $B D$ 为直角边作等腰直角三角形 $B D E$ ， $B E$ 交 $y$ 轴于点 $F$ ．

(1)、当 $A D = 1$ 时，则点 $E$ 坐标为；

(2)、连接 $D F$ ，当点 $D$ 在线段 $O A$ 上运动时， $△ O D F$ 的周长是否改变，若改变，请说明理由；若不变，求出其周长；

(3)、连接 $C E$ ，当点 $D$ 在线段 $O A$ 上运动时，求 $C E$ 的最小值．

查看试题解析