天津市河北区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-20 类型：期末考试

进入出卷网下载

一、单选题

1. 已知函数 $y = \frac{2}{x + 2}$ ，自变量x的取值范围是（　　）

A、x≠2 B、x≠﹣2 C、x＞﹣2 D、x＞2

查看试题解析
2. 正比例函数y＝（m²+1）x经过的象限是（　　）

A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限

查看试题解析
3. 一组数据的方差可以用式子 $s^{2} = \frac{{(x_{1} - 50)}^{2} + {(x_{2} - 50)}^{2} + {(x_{3} - 50)}^{2} + \dots + {(x_{10} - 50)}^{2}}{10}$ 表示，则式子中的数字50所表示的意义是（）

A、这组数据的个数 B、这组数据的平均数 C、这组数据的众数 D、这组数据的中位数

查看试题解析
4. 如果2是方程x²﹣m＝0的一个根，则m的值为（　　）

A、2 B、 $\sqrt{2}$ C、3 D、4

查看试题解析
5. 已知函数 $y = k x (k \neq 0)$ 中y随 $x$ 的增大而减小，则一次函数 $y = 3 k x + k^{2}$ 的图象大致是（）

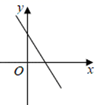A、 B、 C、 D、

查看试题解析
6. 九江某快递公司随着网络的发展，业务增长迅速，完成快递件数从六月份的10万件增长到八月份的12.1万件.假定每月增长率相同，设为x.则可列方程为（）

A、 $10 x + x^{2} = 12.1$ B、 $10 (x + 1) = 12.1$ C、 $10 {(1 + x)}^{2} ＝ 12.1$ D、 $10 + 10 (1 + x) = 12.1$

查看试题解析
7. 若关于x的一元二次方程（k﹣2）x²﹣2kx+k＝0有实数根，则k的取值范围为（　　）

A、k≥0 B、k≥0且k≠2 C、k≥2 D、k≠2

查看试题解析
8. 如图：四个形状大小相同的等腰三角形△ABE ， △ADF ， △CDG ， △BCH按如图摆放在正方形ABCD的内部，顺次连接E、F、G、H得到四边形EFGH ．若∠AEB＝∠AFD＝∠CGD＝∠BHC＝120°，且EH＝ $\sqrt{6}$ ﹣ $\sqrt{2}$ ，则BC的长为（）

A、 $\sqrt{6} + \sqrt{2}$ B、4 $\sqrt{3}$ ﹣4 C、2 $\sqrt{3}$ D、2

查看试题解析

二、填空题

9. 已知点（2，3）在一次函数y＝kx﹣3的图象上，则k＝．

查看试题解析
10. 有一块土地的形状如图所示，∠B=∠D=90°，AB=20m，BC=15m，CD=7m，则这块土地的面积为．

查看试题解析
11. 已知 $y$ 与 $x - 1$ 成正比例，且当 $x = \frac{1}{2}$ 时， $y = - 1$ ，则 $y$ 关于 $x$ 的函数解析式是

查看试题解析
12. 已知P₁（1，y₁），P₂（2，y₂）在正比例函数y＝﹣3x的图象上，则y₁　 y₂（填“＞”或“＜”）．

查看试题解析
13. 已知x₁ ， x₂为方程x²﹣3x﹣7＝0的两个根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ ＝．

查看试题解析
14. 一次函数y₁＝kx＋b与y₂＝x＋a的图象如图所示，若y₁＜y₂ ，则x的取值范围是．

查看试题解析
15. 已知直线y＝（m﹣5）x+m﹣4不经过第三象限，则m的取值范围是．

查看试题解析
16. 如图所示，四边形ABCD中，AC⊥BD于点O，AO=CO=4，BO=DO=3，点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M，作PN⊥DC于点N. 连接PB，在点P运动过程中，PM+PN+PB的最小值等于 .

查看试题解析

三、解答题

17. 选用适当方法解方程：

(1)、x²﹣4x﹣5＝0；

(2)、3x²+x﹣1＝0．

查看试题解析
18. 已知一次函数y＝kx+b的图象由直线y＝﹣2x平移得到，且过点（﹣2，5）．求该一次函数的解析式．

查看试题解析
19. 质量检测部门对公司销售的某电子产品的使用寿命进行跟踪调查，抽查了20件产品，统计结果如表：

时间（年）

6

7

8

9

10

数量（件）

4

6

5

3

2

(1)、这20件产品使用寿命的中位数是，众数是．

(2)、求这20件产品使用寿命的平均数．

(3)、若公司生产了5000件该产品，请你估计使用寿命在9年以上（含9年）的件数．

查看试题解析
20. “疫情”期间，某商场积压了一批商品，现欲尽快清仓，确定降价促销．据调查发现，若每件商品盈利50元时，可售出500件，商品单价每下降1元，则可多售出20件．设每件商品降价x元．

(1)、每件商品降价x元后，可售出商品件（用含x的代数式表示）．

(2)、若要使销售该商品的总利润达到28000元，求x的值．

(3)、销售该商品的总利润能否达到30000元？若能，请求出此时的单价；若不能，请说明理由．

查看试题解析
21. 有两个全等矩形纸条，长与宽分别为11和7，按如图所示的方式交叉叠放在一起，求重合部分构成的四边形BGDH的周长是多少？

查看试题解析
22. 如图，在平面直角坐标系中，边长为3的正方形ABCD在第一象限内，AB∥x轴，点A的坐标为（5，4）经过点O、点C作直线l ，将直线l沿y轴上下平移．

(1)、当直线l与正方形ABCD只有一个公共点时，求直线l的解析式；

(2)、当直线l在平移过程中恰好平分正方形ABCD的面积时，直线l分别与x轴、y轴相交于点E、点F ，连接BE、BF ，求△BEF的面积．

查看试题解析

时间（年）	6	7	8	9	10
数量（件）	4	6	5	3	2