山东省济南市天桥区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-20 类型:期末考试
一、单选题
-
1. 下列地铁标志图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在 , , , , 中,分式的个数为( )个.A、2 B、3 C、4 D、53. 下列因式分解正确的是( ).A、x2-xy+y2=(x+y)2 B、x2-5x-6=(x-2)(x-3) C、x3-4x=x(x2-4) D、9m2-4n2=(3m+2n)(3m-2n)4. 如图,在 中,若 ,则 的度数是( )
2. 在 , , , , 中,分式的个数为( )个.A、2 B、3 C、4 D、53. 下列因式分解正确的是( ).A、x2-xy+y2=(x+y)2 B、x2-5x-6=(x-2)(x-3) C、x3-4x=x(x2-4) D、9m2-4n2=(3m+2n)(3m-2n)4. 如图,在 中,若 ,则 的度数是( ) A、 B、 C、 D、5. 如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件错误的是( )
A、 B、 C、 D、5. 如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件错误的是( ) A、AD=BC B、AB=CD C、AD∥BC D、∠A=∠C6. 在平面直角坐标系中,将点A(5,1)向下平移3个单位,再向右平移2个单位,则平移后A的对应点 的坐标为( )A、 B、 C、 D、7. 一个正多边形的每个外角都是36°,那么它是( )A、正六边形 B、正八边形 C、正十边形 D、正十二边形8. 如图,矩形纸片ABCD中,AB=6 ,BC=8 .现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E , 则CF的长为( )
A、AD=BC B、AB=CD C、AD∥BC D、∠A=∠C6. 在平面直角坐标系中,将点A(5,1)向下平移3个单位,再向右平移2个单位,则平移后A的对应点 的坐标为( )A、 B、 C、 D、7. 一个正多边形的每个外角都是36°,那么它是( )A、正六边形 B、正八边形 C、正十边形 D、正十二边形8. 如图,矩形纸片ABCD中,AB=6 ,BC=8 .现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E , 则CF的长为( )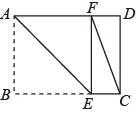 A、3 B、2 C、8 D、109. 如图,在△ABC中,∠ACB=90°,将△ABC绕点C逆时针旋转得到△A1B1C1 , 此时点A的对应点A1恰好在AB边上,点B的对应点为B1 , 则下列结论一定正确的是( )
A、3 B、2 C、8 D、109. 如图,在△ABC中,∠ACB=90°,将△ABC绕点C逆时针旋转得到△A1B1C1 , 此时点A的对应点A1恰好在AB边上,点B的对应点为B1 , 则下列结论一定正确的是( )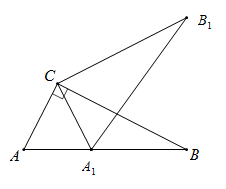 A、AB=B1C B、CA1=A1B C、A1B1⊥BC D、∠CA1A=∠CA1B110. 如图,平行四边形 的周长是 ,对角线 于点,若 ,则 的长等于( )
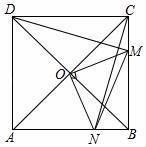
A、AB=B1C B、CA1=A1B C、A1B1⊥BC D、∠CA1A=∠CA1B110. 如图,平行四边形 的周长是 ,对角线 于点,若 ,则 的长等于( ) A、 B、 C、 D、11. 若分式方程 = 无解,则m的值为( )A、0 B、6 C、0或6 D、0或-612. 如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:
A、 B、 C、 D、11. 若分式方程 = 无解,则m的值为( )A、0 B、6 C、0或6 D、0或-612. 如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 分解因式: .14. 如果 = ,那么 =;15. 若分式 的值为0,则x= .16. 已知 是方程 的一个根,则方程的另一个根是 .17. 将正方形A的一个顶点与正方形B的对角线交叉重合,如图1位置,则阴影部分面积是正方形A面积的 ,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的 .

 18. 如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG , 点E为AH的中点,点F为GH的中点,连接EF则EF的最大值与最小值的差为 .
18. 如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG , 点E为AH的中点,点F为GH的中点,连接EF则EF的最大值与最小值的差为 .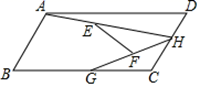
三、解答题
-
19. 解不等式组:20. 先化简再求值: ,其中x= .21. 如图,在 ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
 22.(1)、分解因式:a3-9a;(2)、解方程:x2-4x+1=023. 已知△ABC的三个顶点的坐标分别为 , , .
22.(1)、分解因式:a3-9a;(2)、解方程:x2-4x+1=023. 已知△ABC的三个顶点的坐标分别为 , , .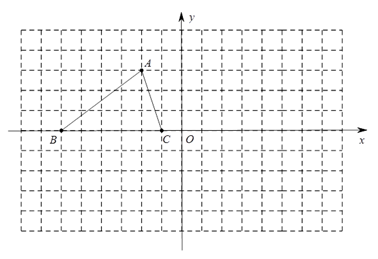 (1)、点A关于y轴对称的点的坐标是;(2)、将△ABC绕坐标原点O顺时针旋转180°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.24. 新冠肺炎疫情防控期间,学校为做好预防消毒工作,开学初购进A,B两种消毒液,购买A种消毒液花费了2500元,购买B种消毒液花费了2000元,且购买A种消毒液数量是购买B种消毒液数量的2倍,已知购买一桶B种消毒液比购买一桶A种消毒液多花30元.(1)、求购买一桶A种、一桶B种消毒液各需多少元?(2)、为了践行“把人民群众生命安全和身体健康摆在第一位”的要求,加强学校防控工作,保障师生健康安全,学校准备再次购买一批防控物资.其中A,B两种消毒液准备购买共50桶.如果学校此次购买A、B两种消毒液的总费用不超过3250元,那么学校此次最多可购买多少桶B种消毒液?25. 如图,四边形ABCD是菱形,DE∥AC , CE∥BD .
(1)、点A关于y轴对称的点的坐标是;(2)、将△ABC绕坐标原点O顺时针旋转180°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.24. 新冠肺炎疫情防控期间,学校为做好预防消毒工作,开学初购进A,B两种消毒液,购买A种消毒液花费了2500元,购买B种消毒液花费了2000元,且购买A种消毒液数量是购买B种消毒液数量的2倍,已知购买一桶B种消毒液比购买一桶A种消毒液多花30元.(1)、求购买一桶A种、一桶B种消毒液各需多少元?(2)、为了践行“把人民群众生命安全和身体健康摆在第一位”的要求,加强学校防控工作,保障师生健康安全,学校准备再次购买一批防控物资.其中A,B两种消毒液准备购买共50桶.如果学校此次购买A、B两种消毒液的总费用不超过3250元,那么学校此次最多可购买多少桶B种消毒液?25. 如图,四边形ABCD是菱形,DE∥AC , CE∥BD .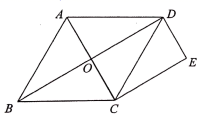 (1)、求证:四边形OCED是矩形.(2)、若∠ABC=60°,AB=2,求矩形OCED周长.(3)、当∠ABC=°时,四边形OCED是正方形.26. 如图1,以平行四边形OABC的顶点O为坐标原点,以OC所在直线为x轴,建立平面直角坐标系,OA=6 ,OC=14,∠AOC=45°,D是对角线AC的中点,点P从点A出发,以每秒1个单位的速度沿AB方向运动到点B , 同时点Q从点0出发,以每秒3个单位的速度沿x轴正方向运动,当点P到达点B时,两个点同时停止运动.
(1)、求证:四边形OCED是矩形.(2)、若∠ABC=60°,AB=2,求矩形OCED周长.(3)、当∠ABC=°时,四边形OCED是正方形.26. 如图1,以平行四边形OABC的顶点O为坐标原点,以OC所在直线为x轴,建立平面直角坐标系,OA=6 ,OC=14,∠AOC=45°,D是对角线AC的中点,点P从点A出发,以每秒1个单位的速度沿AB方向运动到点B , 同时点Q从点0出发,以每秒3个单位的速度沿x轴正方向运动,当点P到达点B时,两个点同时停止运动. (1)、求点A的坐标;(2)、连结PQ , AQ , CP , 当PQ经过点D时,求四边形APCQ的面积.(3)、当以C、D、Q为顶点的三角形是等腰三角形时,点Q的坐标为(直接写出答案即可)27. 在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE .
(1)、求点A的坐标;(2)、连结PQ , AQ , CP , 当PQ经过点D时,求四边形APCQ的面积.(3)、当以C、D、Q为顶点的三角形是等腰三角形时,点Q的坐标为(直接写出答案即可)27. 在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE . (1)、如图1,当点P在线段BD上时,连接CE , BP与CE的数量关系是;CE与AD的位置关系是;(2)、当点P在线段BD的延长线上时,(1)中的结论是否还成立?若成立,请予以证明,若不成立,请说明理由、(请结合图2的情况予以证明或说理.)(3)、如图3,在(2)的条件下,连接BE , 若AB=2,BE= ,求四边形ADPE的面积.
(1)、如图1,当点P在线段BD上时,连接CE , BP与CE的数量关系是;CE与AD的位置关系是;(2)、当点P在线段BD的延长线上时,(1)中的结论是否还成立?若成立,请予以证明,若不成立,请说明理由、(请结合图2的情况予以证明或说理.)(3)、如图3,在(2)的条件下,连接BE , 若AB=2,BE= ,求四边形ADPE的面积.