山东省济南市历下区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-20 类型:期末考试
一、单选题
-
1. 下列四个图分别是山东航空、重庆航空、海南航空和春秋航空公司的标志,其中属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 ,则下列式子正确的是( )A、 B、 C、 D、3. 下列分式中,是最简分式的是( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,已知点 , ,平移线段 ,使点 落在点 处,则点 的对应点 的坐标为( )
2. 若 ,则下列式子正确的是( )A、 B、 C、 D、3. 下列分式中,是最简分式的是( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,已知点 , ,平移线段 ,使点 落在点 处,则点 的对应点 的坐标为( ) A、(0,0) B、(0,-2) C、(-2,0) D、(-3,1)5. 方程 的一个根是 ,则a的值是( )A、6 B、-6 C、8 D、146. 下列说法判断错误的是( )A、对角线相互平分的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线相互垂直平分的四边形是菱形 D、对角线相互垂直且相等的平行四边形是正方形7. 若正多边形的一个外角是40°,则这个正多边形的内角和是( )A、720° B、900° C、1080° D、1260°8. 如图,在 中,对角线 、 交于点 , 是 边的中点,若 的周长为16,则 的周长是( )
A、(0,0) B、(0,-2) C、(-2,0) D、(-3,1)5. 方程 的一个根是 ,则a的值是( )A、6 B、-6 C、8 D、146. 下列说法判断错误的是( )A、对角线相互平分的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线相互垂直平分的四边形是菱形 D、对角线相互垂直且相等的平行四边形是正方形7. 若正多边形的一个外角是40°,则这个正多边形的内角和是( )A、720° B、900° C、1080° D、1260°8. 如图,在 中,对角线 、 交于点 , 是 边的中点,若 的周长为16,则 的周长是( ) A、4 B、6 C、8 D、109. 如图,已知P是∠AOB的平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3 cm,则MD的长度为( )
A、4 B、6 C、8 D、109. 如图,已知P是∠AOB的平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3 cm,则MD的长度为( ) A、3cm B、3 cm C、2cm D、2 cm10. 若关于x的一元二次方程x2﹣x+m=0有两个不相等的实数根,则m的值可能是( )A、2021 B、2 C、1 D、011. 如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,2),则关于x的不等式x+m<kx﹣1的解集在数轴上表示正确的是( )
A、3cm B、3 cm C、2cm D、2 cm10. 若关于x的一元二次方程x2﹣x+m=0有两个不相等的实数根,则m的值可能是( )A、2021 B、2 C、1 D、011. 如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,2),则关于x的不等式x+m<kx﹣1的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、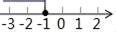 D、
D、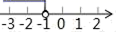 12. 如图,矩形 的顶点 , , 与 轴负半轴的夹角为60°,若矩形绕点 顺时针旋转,每秒旋转60°,则第2021秒时,矩形的对角线交点 的坐标为( )
12. 如图,矩形 的顶点 , , 与 轴负半轴的夹角为60°,若矩形绕点 顺时针旋转,每秒旋转60°,则第2021秒时,矩形的对角线交点 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
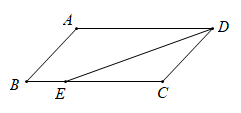
13. 因式分解: .14. 如图,在平行四边形 中, 平分 , , ,则 的周长是.
 15. 方程 的解是 .16. 如图,菱形 的对角线 与 相交于点 ,若 , ,则菱形 的面积为 .
15. 方程 的解是 .16. 如图,菱形 的对角线 与 相交于点 ,若 , ,则菱形 的面积为 . 17. 若 是一元二次方程 的两个实数根,则 的值是.18. 如图, 为边长为2的正方形 的对角线 上任一点,过点 作 于点 , 于点 ,连接 .给出以下4个结论:① ;② ;③ 最短长度为 ;④若 时,则 的长度为2.其中结论正确的有.
17. 若 是一元二次方程 的两个实数根,则 的值是.18. 如图, 为边长为2的正方形 的对角线 上任一点,过点 作 于点 , 于点 ,连接 .给出以下4个结论:① ;② ;③ 最短长度为 ;④若 时,则 的长度为2.其中结论正确的有. 19. 已知点D与点A(0,6)、B(0,﹣4)、C(x , y)是平行四边形的四个顶点,其中x、y满3x﹣4y+12=0,则CD的最小值为 .
19. 已知点D与点A(0,6)、B(0,﹣4)、C(x , y)是平行四边形的四个顶点,其中x、y满3x﹣4y+12=0,则CD的最小值为 .三、解答题
-
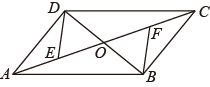
20. 解不等式组:21. 化简: .22. 已知:如图,在 中,对角线 与 相交于点 , , 分别是 和 的中点 .求证: .
 23.(1)、因式分解: ;(2)、解方程: .24. 某市为促进经济发展,增强对外贸易的竞争力,把距离港口360千米的普通公路升级成了同等长度的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2小时,求汽车原来的平均速度.25. 已知:如图,在 中, , 是 的一条角平分线, 是 外角 的平分线, ,垂足为 .连接 交 于点 .
23.(1)、因式分解: ;(2)、解方程: .24. 某市为促进经济发展,增强对外贸易的竞争力,把距离港口360千米的普通公路升级成了同等长度的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2小时,求汽车原来的平均速度.25. 已知:如图,在 中, , 是 的一条角平分线, 是 外角 的平分线, ,垂足为 .连接 交 于点 . (1)、试判断四边形 的形状,并说明理由;(2)、试判断 与 的关系,并说明理由.26. 开发商准备以每平方米20000元价格出售某楼盘,为遵循政府有关房地产的调控政策,开发商经过两次下调销售价格后,决定以每平方米16200元的价格销售.(1)、求平均每次下调的百分率;(2)、房产销售经理向开发商建议:先公布下调5%,再下调15%,这样更有吸引力,请问房产销售经理的方案对购房者是否更优惠?为什么?27. 如图,在四边形 中, , , , ,动点 从点 出发,以 的速度向点 运动,同时动点 从点 出发,以 的速度向点 运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为 秒.
(1)、试判断四边形 的形状,并说明理由;(2)、试判断 与 的关系,并说明理由.26. 开发商准备以每平方米20000元价格出售某楼盘,为遵循政府有关房地产的调控政策,开发商经过两次下调销售价格后,决定以每平方米16200元的价格销售.(1)、求平均每次下调的百分率;(2)、房产销售经理向开发商建议:先公布下调5%,再下调15%,这样更有吸引力,请问房产销售经理的方案对购房者是否更优惠?为什么?27. 如图,在四边形 中, , , , ,动点 从点 出发,以 的速度向点 运动,同时动点 从点 出发,以 的速度向点 运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为 秒. (1)、当四边形 是平行四边形时,求t的值;(2)、当 时,四边形 是矩形;若 且点 的移动速度不变,要使四边形 能够成为正方形,则 点移动速度是 ;(3)、在点 、 运动过程中,若四边形 能够成为菱形,求 的长度.28. (操作发现)
(1)、当四边形 是平行四边形时,求t的值;(2)、当 时,四边形 是矩形;若 且点 的移动速度不变,要使四边形 能够成为正方形,则 点移动速度是 ;(3)、在点 、 运动过程中,若四边形 能够成为菱形,求 的长度.28. (操作发现)
 (1)、如图1,在边长为1个单位长度的小正方形组成的网格中, 的三个顶点均在格点上.
(1)、如图1,在边长为1个单位长度的小正方形组成的网格中, 的三个顶点均在格点上.①请按要求画图:将 绕点 按顺时针方向旋转90°,点 的对应点为 ,点 的对应点为 ;
②连接 ,此时 °;
(2)、(问题解决)在某次数学兴趣小组活动中,小明同学遇到了如下问题:
如图2,在等边 中,点 在内部,且 , , ,求 的长.
经过同学们的观察、分析、思考、交流,对上述问题形成了如下想法:将 绕点 按顺时针方向旋转60°,得到 ,连接 ,寻找 、 、 三边之间的数量关系.…请参考他们的想法,完成该问题的解答过程;
(3)、(学以致用)如图3,在等腰直角 中, , 为 内一点,且 , , ,求 ;
(4)、(思维拓展)注意:从以下①②中,你任意选择一道题解答即可.
①等腰直角 中, , 为 内部一点,若 ,则 的最小值= ▲
②如图4,若点 是正方形 外一点, , , ,求 的度数.
