山东省济南市槐荫区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-20 类型:期末考试
一、单选题
-
1. 下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是( )A、
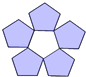 B、
B、 C、
C、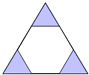 D、
D、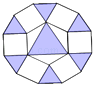 2. 计算 的结果为( )A、a+b B、a-b C、 D、3. 一个多边形的内角和是外角和的 倍,则这个多边形是( )A、六边形 B、五边形 C、四边形 D、七边形4. 如图,矩形ABCD中,AD=10,点P为BC上任意一点,分别连接AP、DP,E、F、G、H分别为AB、AP、DP、DC的中点,则EF+GH的值为( )
2. 计算 的结果为( )A、a+b B、a-b C、 D、3. 一个多边形的内角和是外角和的 倍,则这个多边形是( )A、六边形 B、五边形 C、四边形 D、七边形4. 如图,矩形ABCD中,AD=10,点P为BC上任意一点,分别连接AP、DP,E、F、G、H分别为AB、AP、DP、DC的中点,则EF+GH的值为( ) A、10 B、5 C、2.5 D、无法确定5. 下列因式分解正确的是( )A、 B、 C、 D、6. 若m、n为一元二次方程 的两个实数根,则 的值为( )A、0 B、2 C、3 D、7. 九江某快递公司随着网络的发展,业务增长迅速,完成快递件数从六月份的10万件增长到八月份的12.1万件.假定每月增长率相同,设为x.则可列方程为( )A、 B、 C、 D、8. 如图,在 中, ,在同一平面内,将 绕点A旋转到 的位置,使得 ,则 的度数为( )
A、10 B、5 C、2.5 D、无法确定5. 下列因式分解正确的是( )A、 B、 C、 D、6. 若m、n为一元二次方程 的两个实数根,则 的值为( )A、0 B、2 C、3 D、7. 九江某快递公司随着网络的发展,业务增长迅速,完成快递件数从六月份的10万件增长到八月份的12.1万件.假定每月增长率相同,设为x.则可列方程为( )A、 B、 C、 D、8. 如图,在 中, ,在同一平面内,将 绕点A旋转到 的位置,使得 ,则 的度数为( )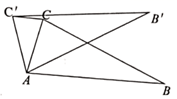 A、30° B、35° C、40° D、50°9. 在▱ABCD中,AC⊥AD,∠B=30°,AC=2,则▱ABCD的周长是( )
A、30° B、35° C、40° D、50°9. 在▱ABCD中,AC⊥AD,∠B=30°,AC=2,则▱ABCD的周长是( ) A、4+2 B、8 C、8+4 D、1610. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形11. 如图,四边形 是边长为8的正方形,点E在边 上, ,过点E作 ,分别交 、 于点G、F , M、N分别是 、 的中点,则 的长是( )
A、4+2 B、8 C、8+4 D、1610. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形11. 如图,四边形 是边长为8的正方形,点E在边 上, ,过点E作 ,分别交 、 于点G、F , M、N分别是 、 的中点,则 的长是( )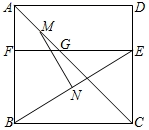 A、4 B、5 C、6 D、712. 如图,在矩形 中, , .点E为射线 上的一个动点, 与 关于直线 对称,当 为直角三角形时,则 的长为( )
A、4 B、5 C、6 D、712. 如图,在矩形 中, , .点E为射线 上的一个动点, 与 关于直线 对称,当 为直角三角形时,则 的长为( )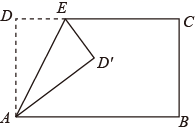 A、2或18 B、3或18 C、3或2 D、2或8
A、2或18 B、3或18 C、3或2 D、2或8二、填空题
-
13. 因式分解:x2+x=14. 若关于x的一元二次方程 的一个根为 ,则另一个根为 .15. 在一个不透明的暗箱中装有红、黄、蓝三种除颜色外完全相同的小球,其中红球5个,黄球7个,蓝球a个.若每次将球充分搅匀后,随机摸出一个小球记下颜色后,放回盒子里,经过大量的重复试验后发现,摸到红球的频率稳定在25%左右,则a的值约为.16. 若关于x的一元二次方程 有两个实数根,则k的取值范围是 .17. 如图,▱ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= BC,连结OE.下列结论:
①∠CAD=30°;②S▱ABCD=AB·AC;③OB=AB;④OE= BC,成立的结论有 . (填序号)
 18. 如图,在菱形 和菱形 中,点A、B、E在同一直线上,P是线段 的中点,连接 、 .若 ,则 的值为 .
18. 如图,在菱形 和菱形 中,点A、B、E在同一直线上,P是线段 的中点,连接 、 .若 ,则 的值为 .
三、解答题
-
19. 解方程: .20. 解分式方程:21. 先化简,再求值: ,其中 .22. 在下面的正方形网格中按要求作图.
 (1)、在图①中将 沿 方向平移,使点A与点C重合,得到 ;(2)、在图②中将 绕点C顺时针旋转90°,得到 .23. 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
(1)、在图①中将 沿 方向平移,使点A与点C重合,得到 ;(2)、在图②中将 绕点C顺时针旋转90°,得到 .23. 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.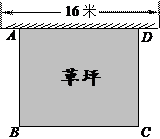 24. 如图, 是 的角平分线,过点作 交 于点E , 交 于点F .
24. 如图, 是 的角平分线,过点作 交 于点E , 交 于点F . (1)、求证:四边形 是菱形;(2)、若 , , ,求菱形 的面积.25. 交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门绘制出2021年五一小长假期间旅游情况统计图,根据以下信息解答下列问题:
(1)、求证:四边形 是菱形;(2)、若 , , ,求菱形 的面积.25. 交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门绘制出2021年五一小长假期间旅游情况统计图,根据以下信息解答下列问题: (1)、五一小长假期间,该市旅游景区景点共接待游客万人,请补全条形统计图 .(2)、根据2021年到该市旅游人数的情况,预计2022年五一小长假期间将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中任选一个景点旅游,求两个旅行团同时选择去同一景点的概率是多少?26. (问题情境)
(1)、五一小长假期间,该市旅游景区景点共接待游客万人,请补全条形统计图 .(2)、根据2021年到该市旅游人数的情况,预计2022年五一小长假期间将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中任选一个景点旅游,求两个旅行团同时选择去同一景点的概率是多少?26. (问题情境)如图1,点E为正方形 内一点, ,将 绕点B顺时针方向旋转90°,得到 (点A的对应点为点C).延长 交 于点F , 连接 .
 (1)、(猜想证明)
(1)、(猜想证明)试判断四边形 的形状,并说明理由;
(2)、如图2,若 ,求证: .(3)、(解决问题)如图3,若 , ,求线段 的长度.
27. 如图1,在平面直角坐标系中,直线y=﹣ x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.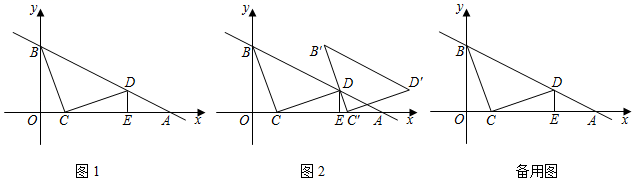 (1)、求证:△BOC≌△CED;(2)、如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;(3)、若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
(1)、求证:△BOC≌△CED;(2)、如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;(3)、若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.