山东省济南市高新区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-20 类型:期末考试
一、单选题
-
1. 在直角坐标系中,点 向左平移3个单位长度后的坐标为( )A、 B、 C、 D、2. 4x2y和6xy3的公因式是( )A、2xy B、3xy C、2x2y D、3xy33. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、4. 如图,四边形 是平行四边形,将 延长至点 ,若 ,则 等于( )
 A、110° B、35° C、80° D、55°5. 菱形的面积为12cm2 , 一条对角线是6cm,那么菱形的另一条对角线长为( )A、3cm B、4cm C、5cm D、6cm6. 一元二次方程 的一个根是0,则 的值是( )A、2 B、1 C、2或-2 D、-27. 一个不透明的袋子中装有除颜色外其余均相同的3个白球,x个黑球,随机的从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀,大量重复试验后,发现摸出白球的频率稳定在0.3附近,则x的值为( )A、2 B、3 C、7 D、138. 计算 的结果是( )A、 B、 C、 D、9. 关于x的一元二次方程 有实数根,则a的取值范围是( )A、 B、 C、 且 D、 且10. 如图,将△ABC先向上平移1个单位,再绕点P按逆时针方向旋转90°,得到△A′B′C′,则点A与点A′的距离是( )
A、110° B、35° C、80° D、55°5. 菱形的面积为12cm2 , 一条对角线是6cm,那么菱形的另一条对角线长为( )A、3cm B、4cm C、5cm D、6cm6. 一元二次方程 的一个根是0,则 的值是( )A、2 B、1 C、2或-2 D、-27. 一个不透明的袋子中装有除颜色外其余均相同的3个白球,x个黑球,随机的从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀,大量重复试验后,发现摸出白球的频率稳定在0.3附近,则x的值为( )A、2 B、3 C、7 D、138. 计算 的结果是( )A、 B、 C、 D、9. 关于x的一元二次方程 有实数根,则a的取值范围是( )A、 B、 C、 且 D、 且10. 如图,将△ABC先向上平移1个单位,再绕点P按逆时针方向旋转90°,得到△A′B′C′,则点A与点A′的距离是( ) A、 B、 C、27 D、2511. 如图,在矩形 中, , ,点 在边 上,若 平分 ,则 ( )
A、 B、 C、27 D、2511. 如图,在矩形 中, , ,点 在边 上,若 平分 ,则 ( )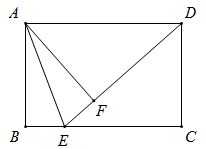 A、 B、 C、 D、12. 如图,已知正方形 的边长为4,P是对角线 上一点, 于点E , 于点F , 连接 ,给出下列结论:① ;②四边形 的周长为8;③ ;④ 的最小值为 ,其中正确结论有几个( )
A、 B、 C、 D、12. 如图,已知正方形 的边长为4,P是对角线 上一点, 于点E , 于点F , 连接 ,给出下列结论:① ;②四边形 的周长为8;③ ;④ 的最小值为 ,其中正确结论有几个( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 分解因式: =.
14. 如图, 的度数为 .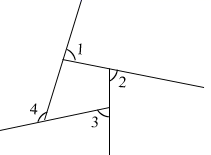 15. 点 与点 关于原点对称,则 .16. 将分式 化简的结果是 .17. 某文具店三月份销售铅笔100支,四,五两个月销售量连续增长.若四,五月平均增长率为x , 则该文具店五月份销售铅笔的支数是 . (用含x的代数式表示)18. 如图等边三角形ABC中,点O是△ABC的∠B和∠C的角平分线的交点,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于点D、E两点,连接DE,若OA=2,则△ODE周长最小值为.
15. 点 与点 关于原点对称,则 .16. 将分式 化简的结果是 .17. 某文具店三月份销售铅笔100支,四,五两个月销售量连续增长.若四,五月平均增长率为x , 则该文具店五月份销售铅笔的支数是 . (用含x的代数式表示)18. 如图等边三角形ABC中,点O是△ABC的∠B和∠C的角平分线的交点,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于点D、E两点,连接DE,若OA=2,则△ODE周长最小值为.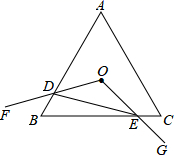
三、解答题
-
19. 解方程: .20. 解方程: .21. 如图,在平行四边形ABCD中,E、F是对角线AC上的两点,AE=CF.求证:四边形BEDF是平行四边形.
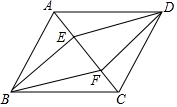 22. 某景区检票口有A、B、C、D共4个检票通道.甲、乙两人到该景区游玩,两人分别从4个检票通道中随机选择一个检票.(1)、甲选择A检票通道的概率是;(2)、求甲乙两人选择的检票通道恰好相同的概率.23. 如图所示,点O是菱形 对角线的交点, , ,连接 ,交 于F .
22. 某景区检票口有A、B、C、D共4个检票通道.甲、乙两人到该景区游玩,两人分别从4个检票通道中随机选择一个检票.(1)、甲选择A检票通道的概率是;(2)、求甲乙两人选择的检票通道恰好相同的概率.23. 如图所示,点O是菱形 对角线的交点, , ,连接 ,交 于F . (1)、求证:四边形 为矩形;(2)、如果 ,求菱形 的面积.24. 某中学兴趣小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边是由周长为30米的篱笆围成.如图所示,已知墙长为20米,设这个苗圃园垂直于墙的一边长为x米
(1)、求证:四边形 为矩形;(2)、如果 ,求菱形 的面积.24. 某中学兴趣小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边是由周长为30米的篱笆围成.如图所示,已知墙长为20米,设这个苗圃园垂直于墙的一边长为x米 (1)、若苗圃园的面积为108m2 , 求x的值,(2)、苗圃园的面积能达到120m2吗?若能,求出x;若不能,说明理由.25. 如图,在平面直角坐标系中,点O为坐标原点,AB∥OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,当一个点到达终点后另一个点继续运动,直至到达终点,设运动时间为t秒.
(1)、若苗圃园的面积为108m2 , 求x的值,(2)、苗圃园的面积能达到120m2吗?若能,求出x;若不能,说明理由.25. 如图,在平面直角坐标系中,点O为坐标原点,AB∥OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,当一个点到达终点后另一个点继续运动,直至到达终点,设运动时间为t秒. (1)、在t=3时,M点坐标 , N点坐标;(2)、当t为何值时,四边形OAMN是矩形?(3)、运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由;(4)、运动过程中,当MN分四边形OABC的面积为1:2两部分时,求出t的值.26. 老师在讲完乘法公式 的多种运用后,要求同学们运用所学知识解答:求代数式 的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
(1)、在t=3时,M点坐标 , N点坐标;(2)、当t为何值时,四边形OAMN是矩形?(3)、运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由;(4)、运动过程中,当MN分四边形OABC的面积为1:2两部分时,求出t的值.26. 老师在讲完乘法公式 的多种运用后,要求同学们运用所学知识解答:求代数式 的最小值?同学们经过交流、讨论,最后总结出如下解答方法:解:
∵ ,
当 时, 的值最小,最小值是0,
∴
当 时, 的值最小,最小值是1,
∴ 的最小值是1.
请你根据上述方法,解答下列各题
(1)、当x=时,代数式 的最小值是;(2)、若 ,当x=时,y有最值(填“大”或“小”),这个值是;(3)、若 ,求 的最小值.27. 如图1,在等边 中, ,点D是直线 上一点,在射线 上取一点E , 使 ,以 为边作等边 ,连接 . (1)、若点D是 的中点,则 , ;(2)、如图2,连接 ,当点D由 中点向点C运动时,请判断 和 的数量关系,并说明理由;(3)、如图3,点D在 延长线上,连接 ,当 时,求 的长.
(1)、若点D是 的中点,则 , ;(2)、如图2,连接 ,当点D由 中点向点C运动时,请判断 和 的数量关系,并说明理由;(3)、如图3,点D在 延长线上,连接 ,当 时,求 的长.