北京市朝阳区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-20 类型:期末考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 以下列各组数为边长,可以构成直角三角形的是( )A、5,12,13 B、1,2,3 C、3,3,3 D、4,5,63. 一个菱形的两条对角线的长度分别是6 cm和8 cm,这个菱形的面积是( )A、12 cm2 B、14 cm2 C、24 cm2 D、48 cm24. 下列计算正确的是( )A、 B、 C、 D、5. 对八年级500名学生某次数学检测的成绩(百分制)进行了两次统计,第一次统计时,系统把一位缺考同学的成绩自动填充为该次检测唯一的零分,第二次统计时,老师删去了这个零分,则以下统计量在这两次统计中一定保持不变的是( )A、平均数 B、众数 C、中位数 D、方差6. 若四边形ABCD是 甲 , 则四边形ABCD一定是 乙 , 甲、乙两空可以填( )A、平行四边形,矩形 B、矩形,菱形 C、菱形,正方形 D、正方形,平行四边形7. 如图,A , B为 的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,在此图中以A , B为顶点的格点矩形共可以画出( )
 A、1个 B、2个 C、3个 D、4个8. 如图,中国国家博物馆收藏了元代制作的计时工具“铜壶滴漏”,这是目前发现形制最大、最完备的一个多级滴漏,从1316年使用到1919年,一直为人民报时、计时.从上至下的四个铜壶依次名为“日壶”、“月壶”、“星壶”、“受水壶”,通过多级滴漏,使得“星壶”中的水可以匀速滴入圆柱形的“受水壶”中,“受水壶”中带有刻度的木箭随着水位匀速上移,对准标尺就能读出相应的时间.在一天中,“受水壶”中的水面高度h与时间t的函数图象可能是( )
A、1个 B、2个 C、3个 D、4个8. 如图,中国国家博物馆收藏了元代制作的计时工具“铜壶滴漏”,这是目前发现形制最大、最完备的一个多级滴漏,从1316年使用到1919年,一直为人民报时、计时.从上至下的四个铜壶依次名为“日壶”、“月壶”、“星壶”、“受水壶”,通过多级滴漏,使得“星壶”中的水可以匀速滴入圆柱形的“受水壶”中,“受水壶”中带有刻度的木箭随着水位匀速上移,对准标尺就能读出相应的时间.在一天中,“受水壶”中的水面高度h与时间t的函数图象可能是( ) A、
A、 B、
B、 C、
C、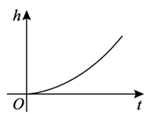 D、
D、
二、填空题
-
9. 若二次根式 在实数范围内有意义,则x的取值范围是 .
10. 请写出一个y随x的增大而减小的正比例函数的表达式 .11. 为了庆祝中国共产党成立100周年,加深同学们对中国共产党历史的认识,激发爱党、爱国热情,某班举行了党史知识竞赛,成绩统计如下表,这组数据的中位数是 .成绩(百分制)
80
85
90
95
100
人数
1
2
5
21
6
12. 一位求职者参加某公司的招聘,面试和笔试的成绩分别是86和90,公司给出他这两项测试的平均成绩为87.6,可知此次招聘中(填“面试”或“笔试”)的权重较大.13. 如图,在△ABC中,点D、E分别是AB、AC的中点.若DE=3,则BC= .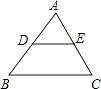 14. 如图,函数y=kx+b(k≠0)的图象经过点(1,2),则不等式kx+b>2的解集为 .
14. 如图,函数y=kx+b(k≠0)的图象经过点(1,2),则不等式kx+b>2的解集为 . 15. 如图,菱形ABCD的对角线AC , BD相交于点O , P为AB边上一动点(不与点A , B重合),PE⊥OA于点E , PF⊥OB于点F , 若AB=4,∠BAD=60°,则EF的最小值为 .
15. 如图,菱形ABCD的对角线AC , BD相交于点O , P为AB边上一动点(不与点A , B重合),PE⊥OA于点E , PF⊥OB于点F , 若AB=4,∠BAD=60°,则EF的最小值为 . 16. 若直线 与两条坐标轴围成的三角形的面积是2,则k的值为 .
16. 若直线 与两条坐标轴围成的三角形的面积是2,则k的值为 .三、解答题
-
17. 计算: .18. 已知:∠AOB .
求作:∠AOB的平分线.
作法:①以点O为圆心,适当长为半径画弧,交OA于点C , 交OB于点D;
②分别以点C , D为圆心,OC长为半径画弧,两弧在∠AOB的内部相交于点P;
③画射线OP .
射线OP即为所求.
 (1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接PC , PD .
由作法可知OC=OD=PC=PD .
∴四边形OCPD是 ▲ .
∴OP平分∠AOB( ▲ )(填推理的依据).
19. 如图,E、F是平行四边形 的对角线 所在直线上的两点,且 ,求证:四边形 是平行四边形. 20. 一次函数的图象经过点(-1,0)和(0,2).(1)、求这个一次函数的表达式;(2)、若直线 与该一次函数的图象相交,且交点在第三象限,直接写出n的取值范围.21. 如图,A , B , H是直线l上的三个点,AC⊥l于点A , BD⊥l于点B , 且HC=HD , AB=5,AC=2,BD=3,求AH的长.
20. 一次函数的图象经过点(-1,0)和(0,2).(1)、求这个一次函数的表达式;(2)、若直线 与该一次函数的图象相交,且交点在第三象限,直接写出n的取值范围.21. 如图,A , B , H是直线l上的三个点,AC⊥l于点A , BD⊥l于点B , 且HC=HD , AB=5,AC=2,BD=3,求AH的长. 22. 在2020年开展的第七次全国人口普查,是在中国特色社会主义进入新时代开展的重大国情国力调查,全面查清中国人口数量、结构、分布、城乡住房等方面的情况,为开启全面建设社会主义现代化国家新征程,向第二个百年奋斗目标进军,提供科学准确的统计信息支持.
22. 在2020年开展的第七次全国人口普查,是在中国特色社会主义进入新时代开展的重大国情国力调查,全面查清中国人口数量、结构、分布、城乡住房等方面的情况,为开启全面建设社会主义现代化国家新征程,向第二个百年奋斗目标进军,提供科学准确的统计信息支持.下面给出了本次调查公布的部分数据:
a . 图1为2010年(第六次)、2020年(第七次)统计的各省、自治区、直辖市的常住人口占全国人口比重的统计图.(注:图1中射线为两轴夹角的角平分线)
b . 图2为七次人口普查中全国人口和年平均增长率的统计图,其中后两次统计中全国人口分为65岁以下人口和65岁及以上人口.


(说明:数据来自国家统计局官方网站,所有数据为大陆所有省、自治区、直辖市和现役军人的人口.)
根据以上信息,回答下列问题:
(1)、从2010年到2020年,常住人口占全国人口的比重增长最多的是广东省,请在图1中用“○”圈出表示广东省的点;(2)、2010年各地区人口比重的方差为 ,2020年各地区人口比重的方差为 ,由图1可知 (填“>”,“<”,“=”).(3)、由图2可知,下列推断合理的是(填写序号).①在这七次调查中,全国人口数量每次都在增加;
②在这七次调查中,从1982年往后,全国人口的年均增长率逐渐下降,说明全国人口每年增加的数量都在减小;
③当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化,从最近两次人口普查数据可以看出,中国老龄化问题日趋严重.
23. 如图,在正方形ABCD中,E为AB边上一点(不与点A , B重合),CF⊥DE于点G , 交AD于点F , 连接BG .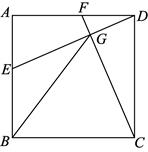
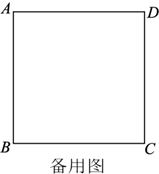 (1)、求证:AE=DF;(2)、是否存在点E的位置,使得△BCG为等腰三角形?若存在,写出一个满足条件的点E的位置并证明;若不存在,说明理由.24. 在数学课上,老师说统计学中常用的平均数不是只有算术平均数一种,好学的小聪通过网络搜索,又得到了两种平均数的定义,他把三种平均数的定义整理如下:
(1)、求证:AE=DF;(2)、是否存在点E的位置,使得△BCG为等腰三角形?若存在,写出一个满足条件的点E的位置并证明;若不存在,说明理由.24. 在数学课上,老师说统计学中常用的平均数不是只有算术平均数一种,好学的小聪通过网络搜索,又得到了两种平均数的定义,他把三种平均数的定义整理如下:对于两个数a , b ,
称为a , b这两个数的算术平均数,
称为a , b这两个数的几何平均数,
称为a , b这两个数的平方平均数.
小聪根据上述定义,探究了一些问题,下面是他的探究过程,请你补充完整:
(1)、若a = -1,b = -2,则M = , N = , P =;(2)、小聪发现当a , b两数异号时,在实数范围内N没有意义,所以决定只研究当a , b都是正数时这三种平均数的大小关系.结合乘法公式和勾股定理的学习经验,他选择构造几何图形,用面积法解决问题:如图,画出边长为a+b的正方形和它的两条对角线,则图1中阴影部分的面积可以表示N2 .



①请分别在图2,图3中用阴影标出一个面积为M2 , P2的图形;
②借助图形可知当a , b都是正数时,M , N , P的大小关系是: ▲ (把M , N , P从小到大排列,并用“<”或“≤”号连接).
25. 对于两个实数a , b , 规定Max(a , b)表示a , b两数中较大者,特殊地,当a = b时,Max(a , b)=a . 如:Max(1,2)= 2,Max(-1,-2)= -1,Max(0,0)=0.(1)、Max(-1,0)= , Max(n , n -2)=;(2)、对于一次函数 , ,①当x≥-1时,Max(y1 , y2)= y2 , 求b的取值范围;
②当x=1-b时,Max(y1 , y2)=p , 当x=1+b时,Max(y1 , y2)=q , 若p≤q , 直接写出b的取值范围.
