广东省深圳市罗湖区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-20 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列四个交通标识图案，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 中国火星探测器“天问一号”成功着陆在火星表面，在距离地球3.2亿公里的遥远星球上，留下了中国行星和深空探测的“脚步”．其中3.2亿用科学记数法表示为（）

A、3.2×10⁷ B、3.2×10⁸ C、3.2×10⁹ D、3.2×10¹⁰

查看试题解析
3. 下列运算正确的是（）

A、x⁵+x⁵＝x¹⁰ B、（﹣3pq）²＝﹣6p²q² C、（a+b）²＝a²+b² D、a^﹣p＝ $\frac{1}{a^{p}}$ （a≠0，p是正整数）

查看试题解析
4. 画△ABC中AB边上的高，下列画法中正确的是（）

A、 AB边上的高CH B、 AB边上的高CH C、 AB边上的高AH D、 AB边上的高AH

查看试题解析
5. 下列各组数据是线段的长度，其中，能构成三角形的是（）

A、1cm ， 2cm ， 3cm B、2cm ， 3cm ， 5cm C、3cm ， 4cm ， 5cm D、3cm ， 3cm ， 6cm

查看试题解析
6. 如图，E是线段AB的中点，∠AEC＝∠DEB ，再添加一个条件，使得△AED≌△BEC ，所添加的条件不正确的是（）

A、AD＝BC B、DE＝CE C、∠A＝∠B D、∠C＝∠D

查看试题解析
7. 一辆公共汽车从车站开出，加速行驶一段时间后开始匀速行驶．过了一段时间，汽车到达下一车站．乘客上、下车后，汽车开始加速，一车站．乘客上、下车后，汽车开始加速，一段时间后又开始匀速行驶．下图中近似地刻画出汽车在这段时间内的速度变化情况的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，将图1边长为a的大正方形的阴影部分剪拼成一个长方形（如图2），这个过程能验证的等式是（）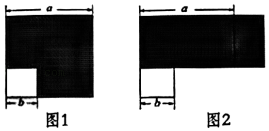

A、（a﹣b）²＝a²﹣2ab+b² B、（a+b）²＝a²+2ab+b² C、a²﹣b²＝（a+b）（a﹣b） D、a （a﹣b）＝a²﹣ab

查看试题解析
9. 下列说法正确的是（）
①两条直线被第三条直线所截，同位角相等；②“在学校运动场上，抛出的篮球会下落”是必然事件；③直线外一点与直线上各点连接的所有线段中，垂线段最短；④角是轴对称图形．

A、①②③④ B、①②③ C、①③④ D、②③④

查看试题解析
10. 如图，一张四边形纸片，AB∥CD ， AC⊥CD ， BD⊥CD ，且AC=BD，连接BC ，点E在CD边上，把△BDE沿直线BE对折，使点D落在线段BC上的点F处，连接AF ．若点A ， E，F在同一条直线上。给出以下结论：
①∠ABE＝∠AB②S_△BEF＝S_△ACF③△ACE≌△BFA④BE＝CE

其中正确的结论共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共15分）

11. 2x²y÷2xy＝．

查看试题解析
12. 如图，直线a∥b ，在Rt△ABC中，点C在直线a上，若∠1＝53°，∠A＝30°，则∠2=°．

查看试题解析
13. 若x²+mx+1是一个完全平方式，则m＝．

查看试题解析
14. 一个小球在光滑度相同的地板上（如图）自由滚动，并随机地停留在某块方砖上，它最终停留在黑砖上的概率是．

查看试题解析
15. 如图，在△ABC中，∠ACB＝90°，点D是BC上的一点，AC＝DC ， AB⊥AE ，且AE=AB，连接DE交AC的延长线于点F ， $\frac{A C}{C F}$ ＝ $\frac{3}{2}$ ，则 $\frac{B D}{C D}$ ＝．

查看试题解析

三、解答题（本大题共7题。其中16题8分，17题6分，18题8分，19题6分，20题7分，21题10分，22题10分，共55分）

16.

(1)、-1²⁰²¹- (- $\frac{1}{2}$ )^-1+ (π -3)⁰+(-2)¹⁰×( $\frac{1}{2}$ )¹⁰

(2)、（x²）³﹣x（x⁵﹣1）．

查看试题解析
17. 先化简，再求值：[（a﹣b）²+（a+b）（a﹣b）]÷2a ，其中a＝2021

查看试题解析
18. 在一个不透明的袋中装有1个红球，2个白球和4个黄球，每个球除颜色外都相同，将球搅匀

(1)、从中任意摸出一个球，摸到红球的概率为；摸到白球的概率为；摸到黄球的概率为；

(2)、若要使得摸到红球的概率是 $\frac{1}{2}$ ，则还要往袋子里添放多个红球．

查看试题解析
19. 如图，△ABC的顶点A ， B ， C都在小正方形的格点上，利用网格线按下列要求画图.

(1)、①画△A₁B₁C₁ ，使它与△ABC关于直线l成轴对称；
②在直线l上求作一点P ，使点A ，点B到它的距离之和最短；

(2)、若网格上的每个小正方形的边长为1，求△ABC的面积．

查看试题解析
20. 如图，把下列的说理过程补充完整：
如图所示，已知AB∥CD ， ∠ABE＝∠DCF ，点O是BC的中点，请问BE与CF相等吗？请说明理由．

解：BE＝CF ．

理由：∵AB∥CD（已知），

∴∠ABC＝∠DCB（   ▲   ），

∵∠ABE＝∠DCF（已知）

∴∠ABC﹣ ▲   ＝∠DCB﹣（   ▲   ）

即∠EBO＝∠FCO

∵点O是BC的中点

∴BO＝CO（中点的概念）

在△BEO和△CFO中

${\begin{cases} ∠ E B O = ∠ F C O (已证) \\ B O = C O (已知) \\ ∠ B O E = ∠ C O F () \end{cases}$

∴△BEO≌△CFO（   ▲   ）

∴BE＝CF（    ▲ ）

查看试题解析
21. 如图，A ， B两地相距50千米，甲于某日下午1时骑自行车从A地出发骑往B地，乙也于同日下午骑摩托车按相同路线从A地出发开往B地，图中的折线PQR和线段EF分别表示甲与乙所行驶的路程s和时间t的关系．根据图象回答下列问题：

(1)、甲出发小时，乙才开始出发；

(2)、乙比甲早到小时；

(3)、甲从下午2时到5时的平均速度是千米/小时；乙的平均速度是千米/小时；

(4)、请你根据图象上的数据，求乙出发后用多长时间就追上甲？

查看试题解析
22. 在△ABC中，∠BAC＝90°，AB＝AC ，点E、点F分别是AB ， AC上（不与B ， C重合）的动点，点O是BC的中点，连接AO ．

(1)、如图1，当∠EOF＝90°时，请问△AEO与△CFO全等吗？如果全等请证明，如果不是请说明理由；

(2)、如图2，在（1）的条件下，过点O作OH⊥AC ，垂足为H，若AE＝3，AF＝9；请求HF的长。

(3)、如图3，当∠EOF＝45°时，连接EF ， 若AO=5，AE：AF：EF＝3：4：5，请求△AOF的面积．

查看试题解析