初中数学华师大版八年级上学期第12章12.3乘法公式同步练习

试卷更新日期：2021-07-19 类型：同步测试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 ${(x - y)}^{2} = x^{2} - y^{2}$ C、 ${(x^{2})}^{3} = x^{6}$ D、 $x^{6} \div x^{3} = x^{2}$

查看试题解析
2. 下列各式能用平方差公式计算的是 $($ 　　 $)$

A、 $(2 a + b) (2 b - a)$ B、 $(- \frac{1}{2} x + 1) (- \frac{1}{2} x - 1)$ C、 $(a + b) (a - 2 b)$ D、 $(2 x - 1) (- 2 x + 1)$

查看试题解析
3. 已知 $a = 2 b - 5$ ，则代数式 $a^{2} - 4 a b + 4 b^{2} - 5$ 的值是（）

A、-30 B、20 C、-10 D、0

查看试题解析
4. 若 $105^{2} - 210 \times 5 + 5^{2} = k + 99^{2} - 1$ ，则 $k$ 的值是（）

A、100 B、105 C、200 D、205

查看试题解析
5. 已知a²-b²+2a+4b-3=0，下列哪个选项可以确定（）

A、a的值 B、b的值 C、a的值和b的值 D、a-b的值或a+b的值

查看试题解析
6. 若a²+ab=7+m，b²+ab=9-m，则a+b的值为（）

A、土4 B、4 C、土2 D 2

查看试题解析
7. 从图1到图2的变化过程可以发现的代数结论是（）

A、（a+b）（a﹣b）＝a²﹣b² B、a²﹣b²＝（a+b）（a﹣b） C、（a+b）²＝a²+2ab+b² D、a²+2ab+b²＝（a+b）²

查看试题解析
8. 观察下列各式及其展开式：（）
${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$

${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$

${(a + b)}^{5} = a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}$

……

你猜想 ${(a + b)}^{10}$ 的展开式第三项的系数是（）

A、66 B、55 C、45 D、36

查看试题解析

二、填空题

9. 计算：(2+x)(2-x)=

查看试题解析
10. 已知a+b＝8，ab＝15，则a²+b²＝．

查看试题解析
11. 阅读材料后解决问题：
小明遇到下面一个问题：计算(2+1)(2²+1)(2⁴+1)(2⁸+1)。

经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：

(2+1)(2²+1)(2⁴+1)(2⁸+1)=(2-1)(2+1)(2²+1)(2⁴+1)(2⁸+1)=(2²-1)(2²+1)(2⁴+1)(2⁸+1)=(2⁴-1)(2⁴+1)(2⁸+1)=(2⁸-1)(2⁸+1)=2¹⁶-1

请你仿照小明解决问题的方法，尝试计算：(6+1)(6²+1)(6⁴+1)(6⁸+1)=。

查看试题解析
12. 现有甲、乙、丙三种不同的矩形纸片（边长如图）．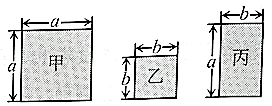

(1)、取甲、乙纸片各1块，其面积和为；

(2)、嘉嘉要用这三种纸片紧密拼接成一个大正方形，先取甲纸片1块，再取乙纸片4块，还需取丙纸片块．

查看试题解析

三、计算题

13. 计算

(1)、|﹣3|﹣（ $\sqrt{3}$ ﹣2）⁰+（ $\frac{1}{2}$ ）^﹣²

(2)、（2a+3）（3﹣2a）

查看试题解析

四、综合题

14. 已知：P＝3a（a+1）﹣（a+1）（a﹣1）

(1)、化简P；

(2)、若a为方程 $\frac{2}{3}$ x²+x﹣ $\frac{5}{3}$ ＝0的解，求P的值．

查看试题解析
15. 阅读理解：对于任意一个四位数，若千位数字与十位数字均为奇数，百位数字与个位数字均为偶数，则称这个四位数为“均衡数”.将一个“均衡数”的千位数字与十位数字组成一个新的两位数m，原来千位数字作为m的十位数字；将一个“均衡数”的百位数字与个位数字组成另一个新的两位数n，原来百位数字作为n的十位数字.例如：“均衡数”3812，则 $m = 31 ， n = 82$ .若 $m ， n$ 各个数位上的数字都不为零且十位数字大于个位数字，则将m中的任意一个数字作为一个新的两位数的十位数字，n中的任意一个数字作为这个新的两位数的个位数字，按这个方式产生的所有新的两位数的和记为 $F (m ， n)$ .例如： $m = 31 ， n = 82$ 时， $F (31 ， 82) = 38 + 32 + 18 + 12 = 100$ .

(1)、3456（填“是”或“不是”）“均衡数”，最小的“均衡数”为；

(2)、若 $F (m ， n)$ 是一个完全平方数，请求出所有满足条件的“均衡数”.

查看试题解析