初中数学华师大版八年级上学期第12章12.2整式的乘法同步练习

试卷更新日期：2021-07-19 类型：同步测试

进入出卷网下载

一、单选题

1. 下列运算中，正确的是（）

A、 $2 a^{2} \cdot a = 2 a^{3}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{2} + a^{3} = a^{5}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
2. 下列代数式中，可以用 $2 x^{2}$ 表示的是（）.

A、 $x^{2} + x^{2}$ B、 $x^{2} \cdot x^{2}$ C、 $2 x \cdot 2 x$ D、 $4 x$

查看试题解析
3. $a^{2} (- a + b - c)$ 与 $a (a^{2} - a b + a c)$ 的关系是（）

A、相等 B、互为相反数 C、前式是后式的-a倍 D、以上结论都不对

查看试题解析
4. 如果 $(x - 2) (x + 3) = x^{2} + p x + q$ ，那么 $p$ ， $q$ 的值分别是（）

A、 $p = 1$ ， $q = - 6$ B、 $p = - 1$ ， $q = - 6$ C、 $p = 5$ ， $q = 6$ D、 $p = - 5$ ， $q = - 6$

查看试题解析
5. 观察下列两个多项式相乘的运算过程：

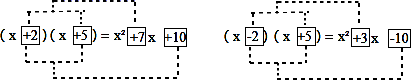
根据你发现的规律，若（x+a）（x+b）=x²-7x+12，则a，b的值可能分别是（）

A、-3，4 B、3，-4 C、-3，-4 D、3，4

查看试题解析
6. 已知a+b＝3，ab＝﹣7，则（a+1）（b+1）的值为（）

A、﹣3 B、﹣21 C、7 D、21

查看试题解析
7. 如图1的8张宽为a，长为 $b (a < b)$ 的小长方形纸片，按如图2的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示.设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（）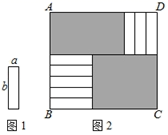

A、 $b = 5 a$ B、 $b = 4 a$ C、 $b = 3 a$ D、 $b = a$

查看试题解析
8. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 ${(a + b)}^{n} (n$ 为非负整数）的展开式中，把各项系数按一定的规律排成右表（展开后每一项按 $a$ 的次数由大到小的顺序排列）．人们把这个表叫做“杨辉三角”．据此规律，则 ${(x + 1)}^{2019}$ 展开式中含 $x^{2018}$ 项的系数是 $($ 　　 $)$

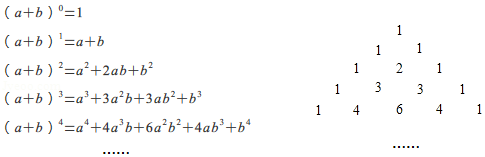A、2016 B、2017 C、2018 D、2019

查看试题解析

二、填空题

9. 计算﹣5a²•2a³的结果等于．

查看试题解析
10. 若 3x(x+1)＝mx²+nx，则 m+n＝.

查看试题解析
11. 已知（2x²﹣3x+a）（x+2）计算结果中不含x项，则a＝．

查看试题解析
12. 如图，现有A，C两类正方形卡片和B类长方形卡片各若干张，用它们可以拼成一些新的长方形．如果要拼成一个长为（3a+b），宽为（a+2b）的长方形，那么需要B类长方形卡片张．

查看试题解析
13. 观察、归纳：
（x﹣1）（x+1）＝x²﹣1；

（x﹣1）（x²+x+1）＝x³﹣1；

（x﹣1）（x³+x²+x+1）＝x⁴﹣1；

…

请你根据以上等式的规律，完成下列问题：

⑴（x﹣1）（xⁿ+…+x²+x+1）＝﹣1；

⑵计算：1+2+2²+…+2²⁰¹⁹＝．

查看试题解析

三、计算题

14. 化简：

(1)、（x+1）（x+2）

(2)、2a²b×（﹣3bc）

查看试题解析

四、综合题

15. 如图，甲长方形的长为m+7，宽为m+1，面积为S₁；乙长方形的长为m+4，宽为m+2，面积为S₂ ．（m为正整数）

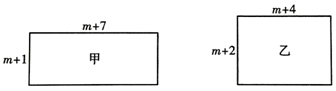(1)、试比较S₁ ， S₂的大小；

(2)、现有一正方形，其周长与图中的甲长方形周长相等，试探究：该正方形面积S与图中的甲长方形面积S₁的差（即S﹣S₁）是一个常数，求出这个常数．

查看试题解析
16.

(1)、有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图所示，化简： $| a + c | - | a - b - c | - | b - c | + | b + c |$ ．

(2)、已知 $a x^{2} + b x + 1$ 与 $2 x^{2} - 3 x + 1$ 的积不含 $x^{3}$ 项和 $x$ 项，求关于 $x$ 的方程 $\frac{a + 2 b}{a} x + \frac{3 a - b}{b} = 0$ 的解．

查看试题解析
17. 观察以下等式：
（x+1）（x²﹣x+1）=x³+1

（x+3）（x²﹣3x+9）=x³+27

（x+6）（x²﹣6x+36）=x³+216

…

(1)、按以上等式的规律，填空：（a+b）（）=a³+b³

(2)、利用多项式的乘法法则，说明（1）中的等式成立．

(3)、利用（1）中的公式化简：（x+y）（x²﹣xy+y²）﹣（x+2y）（x²﹣2xy+4y²）

查看试题解析