四川省泸州市2021届高三理数第二次质量诊断试卷
试卷更新日期:2021-07-19 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 若 ,则 ( )A、 B、 C、2 D、43. 某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图和90后从事互联网行业者岗位分布图(90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生),则下列结论中不一定正确的是( )
整个互联网行业从业者年龄分布饼状图 90后从事互联网行业者岗位分布图

 A、互联网行业从业人员中90后占一半以上 B、互联网行业中从事技术岗位的人数90后比80后多 C、互联网行业中从事设计岗位的人数90后比80前多 D、互联网行业中从事市场岗位的90后人数不足总人数的10%4. 若x,y满足 ,则x+2y的最大值为( )A、1 B、3 C、5 D、95. 离散型随机变量 服从二项分布 ,且 , ,则 的值为( )A、 B、 C、 D、6. 把函数 的图象向右平移 个单位长度得到函数 ,若 在 上是增函数,则 的最大值为( )A、 B、 C、 D、7. 在 中, , ,点 满足 ,则 的值为( )A、-6 B、6 C、-8 D、88. 一个几何体的三视图如图所示,则该几何体的体积为( )
A、互联网行业从业人员中90后占一半以上 B、互联网行业中从事技术岗位的人数90后比80后多 C、互联网行业中从事设计岗位的人数90后比80前多 D、互联网行业中从事市场岗位的90后人数不足总人数的10%4. 若x,y满足 ,则x+2y的最大值为( )A、1 B、3 C、5 D、95. 离散型随机变量 服从二项分布 ,且 , ,则 的值为( )A、 B、 C、 D、6. 把函数 的图象向右平移 个单位长度得到函数 ,若 在 上是增函数,则 的最大值为( )A、 B、 C、 D、7. 在 中, , ,点 满足 ,则 的值为( )A、-6 B、6 C、-8 D、88. 一个几何体的三视图如图所示,则该几何体的体积为( )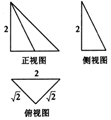 A、 B、 C、 D、19. 已知 , , ,则 , , 的大小关系为( )A、 B、 C、 D、10. 在 中,角 , , 的对边分别为 , , ,若 , ,则 的值为( )A、 B、 C、 D、11. 双曲线 : 的左焦点和虚轴的一个端点分别为 , ,点 为 右支上一动点,若 周长的最小值为 ,则 的离心率为( )A、 B、 C、 D、12. 直六棱柱的底面是正六边形,其体积是 ,则该六棱柱的外接球的表面积的最小值是( )A、 B、 C、 D、
A、 B、 C、 D、19. 已知 , , ,则 , , 的大小关系为( )A、 B、 C、 D、10. 在 中,角 , , 的对边分别为 , , ,若 , ,则 的值为( )A、 B、 C、 D、11. 双曲线 : 的左焦点和虚轴的一个端点分别为 , ,点 为 右支上一动点,若 周长的最小值为 ,则 的离心率为( )A、 B、 C、 D、12. 直六棱柱的底面是正六边形,其体积是 ,则该六棱柱的外接球的表面积的最小值是( )A、 B、 C、 D、二、填空题
-
13. 已知 ,则 .14. 已知函数 ,若 ,则实数 的取值范围是 .15. 过抛物线 的焦点 的直线与该抛物线相交于 , 两点, 为坐标原点,若 ,则 的面积为 .16. 关于函数 有如下四个命题:
①函数 的图象是轴对称图形;
②当 时,函数 有两个零点;
③函数 的图象关于点 中心对称;
④过点 且与曲线 相切的直线可能有三条.
其中所有真命题的序号是 . (填上所有真命题的序号)
三、解答题
-
17. 为了解某水果批发店的日销售量,对过去100天的日销售量进行了统计分析,发现这100天的日销售量都没有超出4.5吨,统计的结果见频率分布直方图.
 (1)、求这100天中日销售量的中位数(精确到小数点后两位);(2)、从这100天中抽取了5天,统计出这5天的日销售量 (吨)和当天的最高气温 (℃)的5组数据 ,研究发现日销售量 和当天的最高气温 具有的线性相关关系,且 , , , .求日销售量 (吨)关于当天最高气温 (℃)的线性回归方程 ,并估计水果批发店所在地区这100天中最高气温在10℃~18℃内的天数.
(1)、求这100天中日销售量的中位数(精确到小数点后两位);(2)、从这100天中抽取了5天,统计出这5天的日销售量 (吨)和当天的最高气温 (℃)的5组数据 ,研究发现日销售量 和当天的最高气温 具有的线性相关关系,且 , , , .求日销售量 (吨)关于当天最高气温 (℃)的线性回归方程 ,并估计水果批发店所在地区这100天中最高气温在10℃~18℃内的天数.参考公式: , .
18. 已知数列 是等比数列, ,且 是 和 的等差中项.(1)、求数列 的通项公式;(2)、设 ,数列 的前 项和为 .求使 成立的最小整数 .19. 如图,已知直四棱柱 的底面是边长为2的正方形, , 分别为 , 的中点. (1)、求证:直线 , , 交于一点;(2)、若直线 与平面 所成的角为 ,求二面角 的余弦值.20. 已知椭圆 : 的离心率为 ,短轴长为 .(1)、求椭圆 的方程;(2)、设不过点 的直线 与 相交于 两点,直线 分别与 轴交于 , 两点,若 ,证明直线 的斜率是定值,并求出该定值.
(1)、求证:直线 , , 交于一点;(2)、若直线 与平面 所成的角为 ,求二面角 的余弦值.20. 已知椭圆 : 的离心率为 ,短轴长为 .(1)、求椭圆 的方程;(2)、设不过点 的直线 与 相交于 两点,直线 分别与 轴交于 , 两点,若 ,证明直线 的斜率是定值,并求出该定值.