山东省2021届高三数学5月份高考联考试卷
试卷更新日期:2021-07-19 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 的元素个数为( )A、0 B、3 C、4 D、52. 在 中,若 ,则 ( )A、3 B、±3 C、4 D、±43. 函数 的图像的切线斜率可能为( )A、 B、-2 C、 D、-44. 跑步是一项有氧运动,通过跑步,我们能提高肌力,同时提高体内的基础代谢水平,加速脂肪的燃烧,养成易瘦体质.小林最近给自己制定了一个200千米的跑步健身计划,他第一天跑了8千米,以后每天比前一天多跑0.5千米,则他要完成该计划至少需要( )A、16天 B、17天 C、18天 D、19天5. 明朝的一个葡萄纹椭圆盘如图(1)所示,清朝的一个青花山水楼阁纹饰椭圆盘如图(2)所示,北宋的一个汝窑椭圆盘如图(3)所示,这三个椭圆盘的外轮廊均为椭圆.已知图(1)、(2)、(3)中椭圆的长轴长与短轴长的比值分别 、 、 ,设图(1)、(2)、(3)中椭圆的离心率分别为 、 、 ,则( )
 A、 B、 C、 D、6. 下列各项中,是 的展开式的项为( )A、15 B、 C、 D、7. 某服装店开张第一周进店消费的人数每天都在变化,设第 天进店消费的人数为y , 且y与 ( 表示不大于t的最大整数)成正比,第1天有10人进店消费,则第4天进店消费的人数为( )A、74 B、76 C、78 D、808. 在三棱柱 中,D为侧棱 的中点,从该三棱柱的九条棱中随机选取两条,则这两条棱所在直线至少有一条与直线 异面的概率是( )A、 B、 C、 D、
A、 B、 C、 D、6. 下列各项中,是 的展开式的项为( )A、15 B、 C、 D、7. 某服装店开张第一周进店消费的人数每天都在变化,设第 天进店消费的人数为y , 且y与 ( 表示不大于t的最大整数)成正比,第1天有10人进店消费,则第4天进店消费的人数为( )A、74 B、76 C、78 D、808. 在三棱柱 中,D为侧棱 的中点,从该三棱柱的九条棱中随机选取两条,则这两条棱所在直线至少有一条与直线 异面的概率是( )A、 B、 C、 D、二、多选题
-
9. 若 ,则( )A、 B、 的最小值为10 C、 D、 的最小值为910. 已知函数 ,则( )A、 的最小正周期为 B、 的图象关于y轴对称 C、 的图象关于 对称 D、 的图象关于 对称11. 已知曲线C的方程为 ,圆 ,则( )A、C表示一条直线 B、当 时,C与圆M有3个公共点 C、当 时,存在圆N , 使得圆N与圆M相切,且圆N与C有4个公共点 D、当C与圆M的公共点最多时,r的取值范围是12. 如图,函数 的图象由一条射线和抛物线的一部分构成, 的零点为 ,则( )
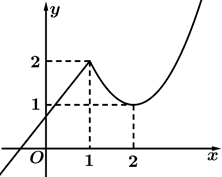 A、函数 有3个零点 B、 恒成立 C、函数 有4个零点 D、 恒成立
A、函数 有3个零点 B、 恒成立 C、函数 有4个零点 D、 恒成立三、填空题
-
13. 写出一个虚数z , 使得 为纯虚数,则 .14. 已知双曲线 的左、右焦点分别为 ,M为C左支上一点,N为线段 上一点,且 ,P为线段 的中点.若 (O为坐标原点),则C的渐近线方程为.15. 2021年受疫情影响,国家鼓励员工在工作地过年.某机构统计了某市5个地区的外来务工人员数与他们选择留在当地过年的人数占比,得到如下的表格:
A区
B区
C区
D区
E区
外来务工人员数
5000
4000
3500
3000
2500
留在当地的人数占比
80%
90%
80%
80%
84%
根据这5个地区的数据求得留在当地过年人员数y与外来务工人员数x的线性回归方程为 .该市对外来务工人员选择留在当地过年的每人补贴1000元,该市F区有10000名外来务工人员,根据线性回归方程估计F区需要给外来务工人员中留在当地过年的人员的补贴总额为万元.(参考数据:取 )
16. 如图,正四棱锥 的每个顶点都在球M的球面上,侧面 是等边三角形.若半球O的球心为四棱锥的底面中心,且半球与四个侧面均相切,则半球O的体积与球M的体积的比值为.
四、解答题
-
17. 的内角 、 、 所对的边分别为 、 、 .已知 , .(1)、若 ,求 ;(2)、若 ,求 的面积.18. 某社区为丰富居民的业余文化生活,打算在周一到周五连续为该社区居民举行“社区音乐会”,每晚举行一场,但若遇到风雨天气,则暂停举行.根据气象部门的天气预报得知,在周一到周五这五天的晚上,前三天每天出现风雨天气的概率均为 ,后两天每天出现风雨天气的概率均为 ,每天晚上是否出现风雨天气相互独立.已知前两天的晚上均出现风雨天气的概率为 ,且这五天至少有一天晚上出现风雨天气的概率为 .(1)、求该社区能举行4场音乐会的概率;(2)、求该社区举行音乐会场数X的数学期望.19. 在数列 中, , ..(1)、求 的通项公式;(2)、在下列两个问题中任选一个作答,如果两个都作答,则按第一个解答计分.
①设 ,数列 的前n项和为 ,证明: .
②设 ,求数列 的前n项和 .
