江西省八校2020-2021学年高二下学期理数第四次联考试卷
试卷更新日期:2021-07-19 类型:月考试卷
一、单选题
-
1. 已知 , ,则 ( )A、 B、 C、 D、2. 设a=log20.4,b=0.42 , c=20.4 , 则a,b,c的大小关系为( )A、a<b<c B、a<c<b C、b<a<c D、b<c<a3. 阅读如图所示的程序框图,运行相应的程序,若输出的 为 ,则判断框中填写的内容可以是( )
 A、 B、 C、 D、4. 屏风文化在我国源远流长,可追溯到汉代.某屏风工艺厂设计了一款造型优美的扇环形屏风,如图,扇环外环弧长为2.4m,内环弧长为0.6 m,径长(外环半径与内环半径之差)为0.9 m,若不计外框,则扇环内需要进行工艺制作的面积的估计值为( )
A、 B、 C、 D、4. 屏风文化在我国源远流长,可追溯到汉代.某屏风工艺厂设计了一款造型优美的扇环形屏风,如图,扇环外环弧长为2.4m,内环弧长为0.6 m,径长(外环半径与内环半径之差)为0.9 m,若不计外框,则扇环内需要进行工艺制作的面积的估计值为( ) A、1.20m2 B、1.25 m2 C、1.35 m2 D、1.40 m25. 从4名男同学和3名女同学中任选2名同学参加志愿者服务,则选出2名同学中恰好有1男1女同学的概率是( )A、 B、 C、 D、6. 函数 的大致图象可能是( )A、
A、1.20m2 B、1.25 m2 C、1.35 m2 D、1.40 m25. 从4名男同学和3名女同学中任选2名同学参加志愿者服务,则选出2名同学中恰好有1男1女同学的概率是( )A、 B、 C、 D、6. 函数 的大致图象可能是( )A、 B、
B、 C、
C、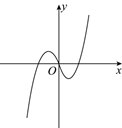 D、
D、 7. 已知实数 满足 则 的最大值为( )A、2 B、 C、4 D、58. 非零向量 , , 满足 , , 的夹角为 , ,则 在 上的投影为( )A、2 B、 C、3 D、49. 已知 为无穷等比数列,且公比 ,记 为 的前 项和,则下面结论正确的是( )A、 B、 C、 是递减数列 D、 存在最小值10. 已知椭圆 : 的左、右焦点分别为 , (如图),过 的直线交 于 , 两点,且 轴, ,则 的离心率为( )
7. 已知实数 满足 则 的最大值为( )A、2 B、 C、4 D、58. 非零向量 , , 满足 , , 的夹角为 , ,则 在 上的投影为( )A、2 B、 C、3 D、49. 已知 为无穷等比数列,且公比 ,记 为 的前 项和,则下面结论正确的是( )A、 B、 C、 是递减数列 D、 存在最小值10. 已知椭圆 : 的左、右焦点分别为 , (如图),过 的直线交 于 , 两点,且 轴, ,则 的离心率为( )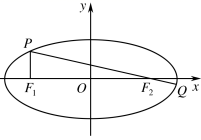 A、 B、 C、 D、11. 已知函数 的图像如图所示,且 的图像关于点 对称,则 的最小值为( )
A、 B、 C、 D、11. 已知函数 的图像如图所示,且 的图像关于点 对称,则 的最小值为( )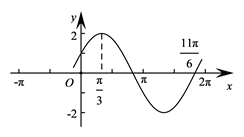 A、 B、 C、 D、12. 如图,已知正四棱柱 的底面边长为1,侧棱长为2,点 , 分别在半圆弧 , (均不含端点)上,且 , , , 在球 上,则下列命题:①当点 在 的三等分点处,球 的表面积为 ;②当点 在 的中点处,过 , , 三点的平面截正四棱柱所得的截面的形状都是四边形;③当点 在 的中点处,三棱锥 的体积为定值.其中真命题的个数为( )
A、 B、 C、 D、12. 如图,已知正四棱柱 的底面边长为1,侧棱长为2,点 , 分别在半圆弧 , (均不含端点)上,且 , , , 在球 上,则下列命题:①当点 在 的三等分点处,球 的表面积为 ;②当点 在 的中点处,过 , , 三点的平面截正四棱柱所得的截面的形状都是四边形;③当点 在 的中点处,三棱锥 的体积为定值.其中真命题的个数为( )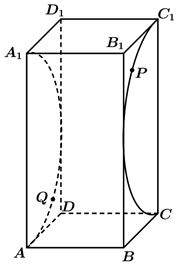 A、3 B、2 C、1 D、0
A、3 B、2 C、1 D、0二、填空题
-
13. 某工厂为了对40个零件进行抽样调查,将其编号为00,01,…,38,39.现要从中选出5个,利用下面的随机数表,从第一行第3列开始,由左至右依次读取,选出来的第5个零件编号是.
0647 4373 8636 9647 3661 4698 6371 6233 2616 8045 6011 1410
9577 7424 6762 4281 1457 2042 5332 3732 2707 3607 5124 5179
14. 设函数 ,若 ,则m= .15. 已知 ,则 .16. 已知双曲线 的左,右焦点分别为 , ,过右焦点 的直线 交该双曲线的右支于 , 两点( 点位于第一象限), 的内切圆半径为 , 的内切圆半径为 ,且满足 ,则直线 的斜率.三、解答题
-
17. 如图,在平面四边形 中, , , .
 (1)、求边 的长;(2)、若 , ,求 的面积.18. 已知公比大于1的等比数列 的前 项和为 ,且 , .(1)、求数列 的通项公式;(2)、在 与 之间插入 个数,使这 个数组成一个公差为 的等差数列,求数列 的前 项和 .19. 如图,四棱锥 中,底面 为直角梯形,其中 , ,面 面 ,且 ,点M在棱AE上.
(1)、求边 的长;(2)、若 , ,求 的面积.18. 已知公比大于1的等比数列 的前 项和为 ,且 , .(1)、求数列 的通项公式;(2)、在 与 之间插入 个数,使这 个数组成一个公差为 的等差数列,求数列 的前 项和 .19. 如图,四棱锥 中,底面 为直角梯形,其中 , ,面 面 ,且 ,点M在棱AE上. (1)、证明:当 时,直线 平面 ;(2)、当 平面 时,求二面角 的余弦值.20. 在某运动会上,有甲队女排与乙队女排以“五局三胜”制进行比赛,其中甲队是“慢热”型队伍,根据以往的经验,首场比赛甲队获胜的概率为 ,决胜局(第五局)甲队获胜的概率为 ,其余各局甲队获胜的概率均为 .(1)、求甲队以 获胜的概率;(2)、现已知甲队以 获胜的概率是 ,若比赛结果为 或 ,则胜利方得3分,对方得0分;若比赛结果为 ,则胜利方得2分,对方得1分,求甲队得分的分布列及数学期望.
(1)、证明:当 时,直线 平面 ;(2)、当 平面 时,求二面角 的余弦值.20. 在某运动会上,有甲队女排与乙队女排以“五局三胜”制进行比赛,其中甲队是“慢热”型队伍,根据以往的经验,首场比赛甲队获胜的概率为 ,决胜局(第五局)甲队获胜的概率为 ,其余各局甲队获胜的概率均为 .(1)、求甲队以 获胜的概率;(2)、现已知甲队以 获胜的概率是 ,若比赛结果为 或 ,则胜利方得3分,对方得0分;若比赛结果为 ,则胜利方得2分,对方得1分,求甲队得分的分布列及数学期望.
