北京市海淀区2021届高三数学模拟试卷（一）

试卷更新日期：2021-07-19 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x + 1 \leq 0}$ ， $B = {x | x \geq a}$ ，若 $A \cup B = R$ ，则实数a的值可以为（）

A、2 B、1 C、0 D、-2

查看试题解析
2. 下列函数值中，在区间 $(0 ， + \infty)$ 上不是单调函数的是（）

A、 $y = x$ B、 $y = x^{2}$ C、 $y = x + \sqrt{x}$ D、 $y = | x - 1 |$

查看试题解析
3. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ .若 $S_{3} = a_{3}$ ，且 $a_{3} \neq 0$ ，则 $\frac{S_{4}}{S_{3}} =$ （）

A、1 B、 $\frac{5}{3}$ C、 $\frac{8}{3}$ D、3

查看试题解析
4. 不等式 $\frac{1}{x} > 1$ 成立的一个充分不必要条件是（）

A、 $0 < x < \frac{1}{2}$ B、 $x > 1$ C、 $0 < x < 1$ D、 $x < 0$

查看试题解析
5. 如图，角 $α$ 以 $O x$ 为始边，它的终边与单位圆 $O$ 相交于点 $P$ ，且点 $P$ 的横坐标为 $\frac{3}{5}$ ，则 $\sin (\frac{π}{2} + α)$ 的值为（）

A、 $- \frac{3}{5}$ B、 $\frac{3}{5}$ C、 $- \frac{4}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（）

A、 $\frac{2 π}{3}$ B、 $\frac{4 π}{3}$ C、 $2 π$ D、 $2 \sqrt{5} π$

查看试题解析
7. 在四边形 $A B C D$ 中， $A B / / C D$ ，设 $\overset{⇀}{A C} = λ \overset{⇀}{A B} + μ \overset{⇀}{A D} (λ ， μ \in R)$ .若 $λ + μ = \frac{3}{2}$ ，则 $\frac{| \overset{⇀}{C D} |}{| \overset{⇀}{A B} |} =$ （）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
8. 已知函数 $f (x) = x^{3} + x^{2} - 2 | x | - k$ .若存在实数 $x_{0}$ ，使得 $f (- x_{0}) = - f (x_{0})$ 成立，则实数 $k$ 的取值范围是（）

A、 $[- 1 ， + \infty)$ B、 $(- \infty ， - 1]$ C、 $[0 ， + \infty)$ D、 $(- \infty ， 0]$

查看试题解析
9. 一个盒中装有大小相同的2个黑球，2个白球，从中任取一球，若是白球则取出来，若是黑球则放回盒中，直到把白球全部取出，则在此过程中恰有两次取到黑球的概率为

A、 $\frac{37}{216}$ B、 $\frac{37}{72}$ C、 $\frac{2}{9}$ D、 $\frac{2}{27}$

查看试题解析
10. 设集合 $A$ 是集合 $N *$ 的子集，对于 $i \in N *$ ，定义 $φ_{i} (A) = {\begin{matrix} 1 ， i \in A \\ 0 ， i \notin A \end{matrix}$ ，给出下列三个结论：①存在 $N *$ 的两个不同子集 $A ， B$ ，使得任意 $i \in N *$ 都满足 $φ_{i} (A \cap B) = 0$ 且 $φ_{i} (A \cup B) = 1$ ；②任取 $N *$ 的两个不同子集 $A ， B$ ，对任意 $i \in N *$ 都有 $φ_{i} (A \cap B) =$ $φ_{i} (A) \cdot$ $φ_{i} (B)$ ；③任取 $N *$ 的两个不同子集 $A ， B$ ，对任意 $i \in N *$ 都有 $φ_{i} (A \cup B) =$ $φ_{i} (A) +$ $φ_{i} (B)$ ；其中，所有正确结论的序号是（）

A、①② B、②③ C、①③ D、①②③

查看试题解析

二、填空题

11. 已知向量 $\overset{⇀}{a} = (1 ， 2) ， \overset{⇀}{b} = (3 ， t)$ ，且 $\overset{⇀}{a} / / \overset{⇀}{b}$ ，则 $t =$

查看试题解析
12. 函数 $f (x) = x - \sqrt{x} - 6$ 的零点个数是

查看试题解析
13. 如图，网格纸上小正方形的边长为 $1$ .从 $A ， B ， C ， D$ 四点中任取两个点作为向量 $\overset{⇀}{b}$ 的始点和终点，则 $\overset{⇀}{a} \cdot \overset{⇀}{b}$ 的最大值为

查看试题解析
14. 已知数列 ${a_{n}}$ 的通项公式为 $a_{n} = \ln n$ ，若存在 $p \in R$ ，使得 $a_{n} \leq p n$ 对任意 $n \in N *$ 都成立，则 $p$ 的取值范围为

查看试题解析
15. 已知函数 $f (x) = \sqrt{2} \sin ω x ， g (x) = \sqrt{2} \cos ω x$ ，其中 $ω > 0$ ， $A ， B ， C$ 是这两个函数图象的交点，且不共线.①当 $ω = 1$ 时， $Δ A B C$ 面积的最小值为；②若存在 $Δ A B C$ 是等腰直角三角形，则 $ω$ 的最小值为.

查看试题解析

三、解答题

16. 在① $a_{1} = 3 ， a_{4} = S_{2}$ ，② $a_{3} = b_{2} ， a_{5} = b_{3} - b_{1}$ ，③ $a_{1} = b_{2} - 2 ， a_{2} = S_{2} - 3$ 这三个条件中任选一个，补充在下面问题中，若问题中的 $λ$ 存在，求 $λ$ 的最小值；若 $λ$ 不存在，说明理由.
设数列 ${a_{n}}$ 为等差数列， $S_{n}$ 是数列 ${b_{n}}$ 的前 $n$ 项和，且 ▲ ， $b_{3} = 8 ， b_{n} = 2 b_{n - 1} (n ⩾ 2 ， n \in N^{*})$ .记 $c_{n} = \frac{1}{a_{n} {log}_{2} b_{n}}$ ， $T_{n}$ 为数列 ${c_{n}}$ 的前 $n$ 项和，是否存在实数 $λ$ ，使得对任意的 $n \in N^{*}$ 都有 $T_{n} < λ ?$

注：如果选择多个条件分别解答，按第一个解答计分.

查看试题解析
17. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为菱形， $∠ A B C = 60 °$ ， $P B = P C$ ， $E$ 为线段 $B C$ 的中点， $F$ 为线段 $P A$ 上的一点.

(1)、证明：平面 $P A E ⊥$ 平面 $B C P$ .

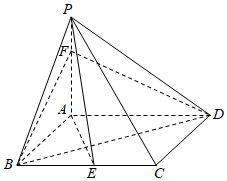(2)、若 $P A = A B = \frac{\sqrt{2}}{2} P B$ ，二面角 $A - B D - F$ 的余弦值为 $\frac{3}{5}$ ，求 $P D$ 与平面 $B D F$ 所成角的正弦值.

查看试题解析
18. 根据某水文观测点的历史统计数据，得到某河流水位 $X$ （单位：米）的频率分布直方图如下.将河流水位在 $[20 ， 22)$ ， $[22 ， 24)$ ， $[24 ， 26)$ ， $[26 ， 28)$ ， $[28 ， 30)$ ， $[30 ， 32)$ ， $[32 ， 34]$ 各段内的频率作为相应段的概率，并假设每年河流水位变化互不影响.

(1)、求未来4年中，至少有2年该河流水位 $x \in [26 ， 30)$ 的概率（结果用分数表示）.

(2)、已知该河流对沿河 $A$ 工厂的影响如下：当 $X \in [20 ， 26)$ 时，不会造成影响；当 $X \in [26 ， 30)$ 时，损失50000元；当 $X \in [30 ， 34]$ 时，损失300000元.为减少损失， $A$ 工厂制定了三种应对方案.
方案一：不采取措施；

方案二：防御不超过30米的水位，需要工程费用8000元；

方案三：防御34米的最高水位，需要工程费用20000元.

试问哪种方案更好，请说明理由.

查看试题解析
19. 已知椭圆 $C$ 的中心在原点， $F (1 ， 0)$ 是它的一个焦点，直线 $l_{1}$ ，过点 $F$ 与椭圆 $C$ 交于 $A$ ， $B$ 两点，当直线 $l_{1} ⊥ x$ 轴时， $\overset{⇀}{O A} \cdot \overset{⇀}{O B} = \frac{1}{2}$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、设椭圆的左顶点为 $P$ ， $P A$ 、 $P B$ 的延长线分别交直线 $l_{2} ： x = 2$ 于 $M$ ， $N$ 两点，证明：以 $M N$ 为直径的圆过定点。

查看试题解析
20. 已知函数 $f (x) = \frac{\ln x}{e^{x}}$ .

(1)、判断函数 $f (x)$ 在区间 $(0 ， 1)$ 上的单调性，并说明理由；

(2)、求证： $f (x) < \frac{1}{2}$ .

查看试题解析
21. 已知集合 $M \subseteq N *$ ，且 $M$ 中的元素个数 $n$ 大于等于5.若集合 $M$ 中存在四个不同的元素 $a ， b ， c ， d$ ，使得 $a + b = c + d$ ，则称集合 $M$ 是“关联的”，并称集合 ${a ， b ， c ， d}$ 是集合 $M$ 的“关联子集”；若集合 $M$ 不存在“关联子集”，则称集合 $M$ 是“独立的”.

(1)、分别判断集合 ${2 ， 4 ， 6 ， 8 ， 10}$ 和集合 ${1 ， 2 ， 3 ， 5 ， 8}$ 是“关联的”还是“独立的”？若是“关联的”，写出其所有的关联子集；

(2)、已知集合 ${a_{1} ， a_{2} ， a_{3} ， a_{4} ， a_{5}}$ 是“关联的”，且任取集合 ${a_{i} ， a_{j}} \subseteq M$ ，总存在 $M$ 的关联子集 $A$ ，使得 ${a_{i} ， a_{j}} \subseteq A$ .若 $a_{1} < a_{2} < a_{3} < a_{4} < a_{5}$ ，求证： $a_{1} ， a_{2} ， a_{3} ， a_{4} ， a_{5}$ 是等差数列；

(3)、集合 $M$ 是“独立的”，求证：存在 $x \in M$ ，使得 $x > \frac{n^{2} - n + 9}{4}$ .

查看试题解析