“陕西名校”2021届高三理数5月检测试卷
试卷更新日期:2021-07-19 类型:高考模拟
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 复数 的共轭复数为( )A、 B、 C、 D、3. 袋中有红、黄、绿,蓝颜色的球各一个,每次随机取一个后放回袋中,连续取四次,则取出的球颜色完全不相同的概率为( )A、 B、 C、 D、4. 已知实数 满足约束条件 ,则目标函数 的最小值为( )A、-5 B、 C、 D、45. 已知 是定义在 上的奇函数,且在 上单调递增,若 ,则下列不等式错误的是( )A、 B、 C、 D、6. 已知 ,则 ( )A、 B、-1 C、1 D、27. 如图,边长都为 的正方形 与正方形 的中心分别为 ,点 分别是 的中点,则 ( )
 A、-4 B、8 C、10 D、8. 如图所示的是某多面体的三视图,其中A和B分别对应该多面体的两个顶点,则这两个顶点的距离为( )
A、-4 B、8 C、10 D、8. 如图所示的是某多面体的三视图,其中A和B分别对应该多面体的两个顶点,则这两个顶点的距离为( ) A、 B、2 C、 D、9. 已知在 中,角 的对边分别为 则 边上的高为( )A、1 B、 C、 D、210. 已知函数 图象的相邻两条对称轴间的距离为 ,且 ,则不等式 的解集为( )A、 B、 C、 D、11. 设 分别为双曲线 的左、右焦点,双曲线上存在一点 使得 ,则该双曲线的离心率为( )A、 B、3 C、 D、12. 卢浮宫金字塔位于巴黎卢浮宫的主院,由美籍华人建筑师贝聿铭设计,已成为巴黎的城市地标.金字塔为正四棱锥造型,该正四棱锥的底面边长为 ,高为 ,若该四棱锥的五个顶点都在一个球面上,则球心到四棱锥侧面的距离为( )
A、 B、2 C、 D、9. 已知在 中,角 的对边分别为 则 边上的高为( )A、1 B、 C、 D、210. 已知函数 图象的相邻两条对称轴间的距离为 ,且 ,则不等式 的解集为( )A、 B、 C、 D、11. 设 分别为双曲线 的左、右焦点,双曲线上存在一点 使得 ,则该双曲线的离心率为( )A、 B、3 C、 D、12. 卢浮宫金字塔位于巴黎卢浮宫的主院,由美籍华人建筑师贝聿铭设计,已成为巴黎的城市地标.金字塔为正四棱锥造型,该正四棱锥的底面边长为 ,高为 ,若该四棱锥的五个顶点都在一个球面上,则球心到四棱锥侧面的距离为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 曲线 在 处的切线方程为.14. 的展开式中, 的系数为.15. 已知抛物线 焦点为 为坐标原点,直线 过点 与抛物线交于 两点,与 轴交于 ,若 ,则 的面积为.16. 已知 ,设函数 若关于 的不等式 在 上恒成立,则 的取值范围.
三、解答题
-
17. 某社区随机选取了部分居民,调查他们对今年春节期间社区组织文艺和体育活动的意见(每人只选择其中一项),调查结果如下表所示:
文艺活动
体育活动
男性居民
15
20
女性居民
25
10
(1)、判断能否有95%的把握认为居民选择的活动类型与性别有关;(2)、用分层抽样方法,在样本中选择文艺活动的居民中按性别抽取8人,再从这8人中随机选3人,记这3人中男性居民的人数为 ,求 的分布列和数学期望.附: ,其中 .
P(K2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
18. 已知公差不为0的等差数列 满足 ,且 成等比数列.(1)、求 的通项公式;(2)、设 ,求数列 的前 项和 .19. 如图,在正三棱柱 中, 分别是 的中点.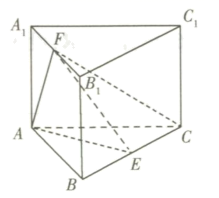 (1)、求证: 平面 ;(2)、求二面角 的余弦值.20. 已知函数(1)、若 对任意 恒成立,求 的最大值;(2)、若 ,求 在 上的极值点的个数.
(1)、求证: 平面 ;(2)、求二面角 的余弦值.20. 已知函数(1)、若 对任意 恒成立,求 的最大值;(2)、若 ,求 在 上的极值点的个数.