初中数学华师大版九年级上学期第22章22.2.2配方法同步练习

试卷更新日期：2021-07-16 类型：同步测试

进入出卷网下载

一、单选题

1. 用配方法解方程x²﹣4x＝1时，原方程应变形为（）

A、（x﹣2）²＝1 B、（x+2）²＝5 C、（x+2）²＝1 D、（x﹣2）²＝5

查看试题解析
2. 给出以下方程的解题过程，其中正确的有（）
①解方程 $\frac{1}{2}$ （x﹣2）²＝16，两边同时开方得x﹣2＝±4，移项得x₁＝6，x₂＝﹣2；②解方程x（x﹣ $\frac{1}{2}$ ）＝（x﹣ $\frac{1}{2}$ ），两边同时除以（x﹣ $\frac{1}{2}$ ）得x＝1，所以原方程的根为x₁＝x₂＝1；③解方程（x﹣2）（x﹣1）＝5，由题得x﹣2＝1，x﹣1＝5，解得x₁＝3，x₂＝6；④方程（x﹣m）²＝n的解是x₁＝m+ $\sqrt{n}$ ，x₂＝m﹣ $\sqrt{n}$ ．

A、0个 B、2个 C、3个 D、4个

查看试题解析
3. 若方程x²﹣8x+m＝0可通过配方写成（x﹣n）²＝6的形式，则x²+8x+m＝5可配方成（）

A、（x﹣n+5）²＝1 B、（x+n）²＝1 C、（x﹣n+5）²＝11 D、（x+n）²＝11

查看试题解析
4. 用配方法解下列方程时，配方有错误的是（）．

A、x²-2x-99=0化为(x-1)²=100 B、x²+8x+9=0化为(x+4)²=25 C、2t²-7t-4=0化为 ${(t - \frac{7}{4})}^{2} = \frac{81}{16}$ D、3y²-4y-2=0化为 ${(y - \frac{2}{3})}^{2} = \frac{10}{9}$

查看试题解析
5. 下列用配方法解方程 $\frac{1}{2} x^{2} - x - 2 = 0$ 的四个步骤中，出现错误的是（）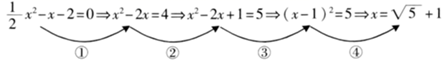

A、① B、② C、③ D、④

查看试题解析
6.
把一元二次方程 $x^{2} + 6 x + 4 = 0$ 化成 $(x + m)^{2} = n$ 的形式，则 $m + n$ 的值（）

A、3 B、5 C、6 D、8

查看试题解析
7. 欧几里得是古希腊数学家，所著的《几何原本》闻名于世．在《几何原本》中，形如x²+ax＝b²的方程的图解法是：如图，以 $\frac{a}{2}$ 和b为直角边作Rt△ABC，再在斜边上截取BD＝ $\frac{a}{2}$ ，则图中哪条线段的长是方程x²+ax＝b²的解？答：是（）

A、AC B、AD C、AB D、BC

查看试题解析

二、填空题

8. 用配方法解方程 $2 x^{2} - x = 4$ ，配方后方程可化为 ${(x - \frac{1}{4})}^{2} =$ ．

查看试题解析
9. 将一元二次方程 $x^{2} - 3 x + 1 = 0$ 变形为 ${(x + h)}^{2} = k$ 的形式为.

查看试题解析
10. 将一元二次方程x²-8x-5=0化成 $（ x + a)^{2} = b$ 的形式，则 $3 a - b$ = ．

查看试题解析
11. 对于实数m ， n ，我们定义一种运算为：m※n＝mn+m﹣n ，则（a+b）※（a﹣b）＝，则方程x※（2※x）＝﹣3的解是．

查看试题解析
12. 已知x，y，z为实数，且2x﹣3y+z=3，则x²+（y﹣1）²+z²的最小值为．

查看试题解析

三、计算题

13. 按要求解下列方程：

(1)、（2x﹣3）²+x（2x﹣3）＝0（因式分解法）；

(2)、2x²﹣4x﹣1＝0（用配方法）．

查看试题解析

四、综合题

14. 根据要求，解答下列问题．

(1)、根据要求，解答下列问题．
①方程x²－2x＋1＝0的解为；

②方程x²－3x＋2＝0的解为；

③方程x²－4x＋3＝0的解为；

…… ……

(2)、根据以上方程特征及其解的特征，请猜想：
①方程x²－9x＋8＝0的解为；

②关于x的方程的解为x₁＝1，x₂＝n．

(3)、请用配方法解方程x²－9x＋8＝0，以验证猜想结论的符合题意性．

查看试题解析
15. 嘉淇准备完成题目：解一元二次方程： $x^{2} - 6 x + “ □ ” = 0$ ，

(1)、若“ $□$ ”表示常数－7，请你用配方法解方程： $x^{2} - 6 x - 7 = 0$ ；

(2)、若“ $□$ ”表示一个字母，且一元二次方程 $x^{2} - 6 x + " □ " = 0$ 有实数根，求“ $□$ ”的最大值；

(3)、在（2）的条件下，直接写出方程的解．

查看试题解析