上海市松江区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 直线 在 轴上的截距是( )A、-3 B、2 C、3 D、2. 下列方程中,有实数解的是( )A、 B、 C、 D、3. 下列事件中,确定事件是( )A、掷一枚均匀硬币,正面朝上 B、地球总是绕着太阳转 C、买一注彩票,中奖了 D、小明上学经过红绿灯路口时遇到红灯4. 菱形具有,而矩形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相垂直5. 下列等式一定正确的是( )A、 B、 C、 D、6. 下列命题中,真命题是( )A、四个内角为 、 、 和 的四边形是一定是平行四边形 B、一条对角线被另一条对角线平分的四边形是平行四边形 C、一组对边相等,另一组对边平行的四边形是平行四边形 D、一组对角相等,一组对边平行的四边形是平行四边形
二、填空题
-
7. 方程 的解是 .8. 方程 的解是 .9. 关于 的方程 的解是 .10. 用换元法解方程 时,可设 ,那么原方程可化为关于 的整式方程是 .11. 一个不透明的口袋中有3个红球,2个白球和1个黑球,它们除颜色外完全相同,从中任意摸出一个球,则摸出的是白球的概率是.12. 已知 的周长为 ,点 , , 分别为 三条边的中点,则 的周长为 .13. 一个多边形的内角和是720°,这个多边形的边数是 .14. 直线 沿 轴向上平移3个单位得到的直线表达式是 .15. 如果一次函数 ( 是常数, )的图象过点 ,那么 的值随 的增大而(填“增大”或“减小”).16. 一次函数 ( , 为常数)的图像如图所示,那么关于 的一元一次不等式 的解集是 .
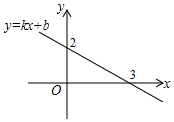 17. 在平面直角坐标系 中,已知四边形 是平行四边形,点 、 、 ,那么点 的坐标为 .18. 如图,将矩形 的四个角向内折起,恰好拼成一个无缝隙重叠的四边形 ,若 , ,则边 的长是 .
17. 在平面直角坐标系 中,已知四边形 是平行四边形,点 、 、 ,那么点 的坐标为 .18. 如图,将矩形 的四个角向内折起,恰好拼成一个无缝隙重叠的四边形 ,若 , ,则边 的长是 .
三、解答题
-
19. 解方程:20. 解方程:21. 如图,点 是菱形 边 的延长线上的一点, ,设 , .
 (1)、试用向量 , 表示下列向量: =;(直接写出结论)(2)、如果 , ,那么 =;(直接写出结论)(3)、在图上求作: .(保留作图痕迹,不要求写作法,写出结论).22. 今年初,很多商场由于受新型冠状病毒肺炎疫情的影响,产品销售情况不如人意.有甲、乙两家商场利用网络平台进行销售.其中甲商场所有商品按 折出售,乙商场对一次购物中超过 元后的金额打 折( 为 到 之间的整数).设顾客所购商品原来金额为 元,在甲、乙两家商场实际支付金额分别为 元和 元.
(1)、试用向量 , 表示下列向量: =;(直接写出结论)(2)、如果 , ,那么 =;(直接写出结论)(3)、在图上求作: .(保留作图痕迹,不要求写作法,写出结论).22. 今年初,很多商场由于受新型冠状病毒肺炎疫情的影响,产品销售情况不如人意.有甲、乙两家商场利用网络平台进行销售.其中甲商场所有商品按 折出售,乙商场对一次购物中超过 元后的金额打 折( 为 到 之间的整数).设顾客所购商品原来金额为 元,在甲、乙两家商场实际支付金额分别为 元和 元. (1)、顾客在乙商场购物时, 与 之间函数图象如图所示(图中线段 和射线 ),求当 时, 与 之间函数解析式;(2)、当 时,甲、乙两个商场中,去哪家商场购物更省钱?23. 如图,已知等腰梯形 中, , 、 分别是两腰的中点,联结 ,过点 作 ,交 于点 ,联结 .
(1)、顾客在乙商场购物时, 与 之间函数图象如图所示(图中线段 和射线 ),求当 时, 与 之间函数解析式;(2)、当 时,甲、乙两个商场中,去哪家商场购物更省钱?23. 如图,已知等腰梯形 中, , 、 分别是两腰的中点,联结 ,过点 作 ,交 于点 ,联结 . (1)、求证:四边形 是平行四边形;(2)、当 时,求证:四边形 是矩形.24. 甲乙两人各加工300个零件,甲比乙少用1小时完成任务;乙改进操作方法,使生产效率提高了一倍,结果乙完成300个零件所用的时间比甲完成250个零件所用的时间少 小时.问甲乙两人原来每小时各加工多少个零件.25. 在一次数学研究性学习中,小明将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图 ).其中 , , .并进行如下研究活动:将图 中的纸片 沿 方向平移,联结 , (如图 ).
(1)、求证:四边形 是平行四边形;(2)、当 时,求证:四边形 是矩形.24. 甲乙两人各加工300个零件,甲比乙少用1小时完成任务;乙改进操作方法,使生产效率提高了一倍,结果乙完成300个零件所用的时间比甲完成250个零件所用的时间少 小时.问甲乙两人原来每小时各加工多少个零件.25. 在一次数学研究性学习中,小明将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图 ).其中 , , .并进行如下研究活动:将图 中的纸片 沿 方向平移,联结 , (如图 ). (1)、求证:图2中的四边形 是平行四边形;(2)、当纸片 平移到某一位置时,小明发现四边形 为矩形(如图3).求此时 的长:(3)、在纸片 平移的过程中,四边形 能成为菱形吗?如果可以直接写出 的长,如果不可以,说明理由.26. 如图,已知点 、 分别是正方形 边 以及边 延长线上的点(与正方形顶点不重合),满足 .联结 ,交对角线 于点 .
(1)、求证:图2中的四边形 是平行四边形;(2)、当纸片 平移到某一位置时,小明发现四边形 为矩形(如图3).求此时 的长:(3)、在纸片 平移的过程中,四边形 能成为菱形吗?如果可以直接写出 的长,如果不可以,说明理由.26. 如图,已知点 、 分别是正方形 边 以及边 延长线上的点(与正方形顶点不重合),满足 .联结 ,交对角线 于点 .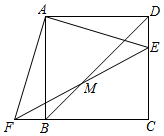 (1)、联结 , ,求证: ;(2)、求证: ;(3)、如果正方形边长为 ,设 , 的面积为 ,求 关于 的函数关系式.
(1)、联结 , ,求证: ;(2)、求证: ;(3)、如果正方形边长为 ,设 , 的面积为 ,求 关于 的函数关系式.