上海市黄浦区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 下列方程中,是无理方程的为( )A、 B、 C、 D、2. 下列方程中,有实数解的是( )A、 B、 C、 D、3. 已知在四边形 中, ,下列可以判定四边形是正方形的是( )A、 B、 C、 D、4. 顺次连结等腰梯形各边中点,所得的四边形一定是( ).A、矩形 B、菱形 C、正方形 D、梯形5. 下列事件中,必然事件是( )A、 是一次函数 B、 是一次函数 C、 是一次函数 D、 ( 是常数)是一次函数6. 如图,将正方形 绕点 逆时针旋转 得到 .如果 ,点 与 的距离为( )
 A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
7. 方程 的根是 .8. 已知关于 的方程 ,如果设 ,那么原方程化为关于 的整式方程是 .9. 方程 的解为 .
10. 如图,一次函数 的图像与 轴、 轴分别相交于 两点,那么当 时,自变量 的取值范围是 . 11. 在 中,点 是边 的中点,如果 ,那么12. 2名男生和2名女生抓阄分派2张电影票,恰好2名女生得到电影票的概率是 .13. 如果一个五边形的每一个内角都相等,那么它的一个内角的度数等于度.14. 已知菱形的边长为13,一条对角线长为10,那么它的面积等于 .15. 如图, 为正方形 外一点, 交 于点 ,则 .
11. 在 中,点 是边 的中点,如果 ,那么12. 2名男生和2名女生抓阄分派2张电影票,恰好2名女生得到电影票的概率是 .13. 如果一个五边形的每一个内角都相等,那么它的一个内角的度数等于度.14. 已知菱形的边长为13,一条对角线长为10,那么它的面积等于 .15. 如图, 为正方形 外一点, 交 于点 ,则 . 16. 若梯形的中位线被它的两条对角线三等分,则梯形的上底与下底之比是17. 如图,平行四边形ABCD中,∠B=60°,AB=8cm , AD=10cm , 点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P , Q运动的速度都为每秒1cm , 那么当运动时间t=秒时,四边形ABPQ是直角梯形.
16. 若梯形的中位线被它的两条对角线三等分,则梯形的上底与下底之比是17. 如图,平行四边形ABCD中,∠B=60°,AB=8cm , AD=10cm , 点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P , Q运动的速度都为每秒1cm , 那么当运动时间t=秒时,四边形ABPQ是直角梯形. 18. 如图,在 中, ,点 在 边上,将 沿直线 翻折后,点 落在点 处,如果四边形BCDE是平行四边形,那么 .
18. 如图,在 中, ,点 在 边上,将 沿直线 翻折后,点 落在点 处,如果四边形BCDE是平行四边形,那么 .
三、解答题
-
19. 解方程: .20. 解方程组: .21. 如图,点 在平行四边形 的对角线 的延长线上.
 (1)、填空: ;
(1)、填空: ;;
(2)、求作: (不写作法,保留作图痕迹,写出结果).22. 某中学八年级学生到离学校15千米的青少年营地举行庆祝十四岁生日活动,先遣队与大部队同时从学校出发.已知先遣队每小时比大部队多行进1千米,预计比大部队早半小时到达目的地.求先遣队与大部队每小时各行进了多少千米.23. 某医药研究所开发了一种新药,在检验药效时发现,如果成人按规定剂量服用,那么服药 时后血液中含药量最高,达 微克/毫升,接着逐步衰减,服药 时后血液中含药盘达 微克/毫升,每毫升血液中含药盘 (微克)随着时间 (时)的变化如图所示. (1)、当成人按规定剂量服用时,求出 时, 与 之间的函数关系式;(2)、如果每毫升血液中含药量为 微克或 微克以上时,治疗疾病是有效的,那么有效时间有多长?24. 如图,在四边形 中, ,点 为 的中点.
(1)、当成人按规定剂量服用时,求出 时, 与 之间的函数关系式;(2)、如果每毫升血液中含药量为 微克或 微克以上时,治疗疾病是有效的,那么有效时间有多长?24. 如图,在四边形 中, ,点 为 的中点.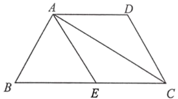 (1)、求证:四边形 是菱形;(2)、联结 ,如果 平分 , 求 的长.
(1)、求证:四边形 是菱形;(2)、联结 ,如果 平分 , 求 的长.