上海市奉贤区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-15 类型：期末考试

进入出卷网下载

一、单选题

1. 一次函数y＝6x﹣1的图像不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 如果关于x的方程ax＝b有无数个解，那么a、b满足的条件是（）

A、a＝0，b＝0 B、a＝0，b≠0 C、a≠0，b＝0 D、a≠0，b≠0

查看试题解析
3. 投掷一枚质地均匀且六个面上分别刻有点数1到6的正方体骰子，观察骰子落地后向上面的点数，下列结果属于必然事件的是（）

A、出现的点数是偶数 B、出现的点数是合数 C、出现的点数是4的倍数 D、出现的点数是60的因数

查看试题解析
4. 如果一个四边形四个内角的度数之比是1：2：2：3，那么这个四边形是（）

A、平行四边形 B、矩形 C、直角梯形 D、等腰梯形

查看试题解析
5. 若 $\vec{A B}$ 是非零向量，则下列等式正确的是（）

A、 $\vec{A B} = \vec{B A}$ ； B、 $| \vec{A B} | = | \vec{B A} |$ ； C、 $\vec{A B} + \vec{B A} = 0$ ； D、 $| \vec{A B} | + | \vec{B A} | = 0$ .

查看试题解析
6. 已知AC、BD是四边形ABCD的两条对角线．如果将“AC⊥BD”记为①，“四边形ABCD是矩形”记为②，“四边形ABCD是菱形”记为③，那么下列判断正确的是（）

A、由①推出② B、由①推出③ C、由②推出① D、由③推出①

查看试题解析

二、填空题

7. 如果将直线y＝x﹣2向上平移2个单位，那么所得直线的表达式是．

查看试题解析
8. 如果一次函数y＝（a﹣1）x+3的函数值y随自变量x的增大而减小，那么a的取值范围是．

查看试题解析
9. 直线 $y = 2 x - 1$ 与 $x$ 轴交点坐标为．

查看试题解析
10. 方程 $\frac{1}{3}$ x³＝9的解是．

查看试题解析
11. 用换元法解方程组 ${\begin{matrix} \frac{5}{x} - \frac{6}{y + 1} = 1 \\ \frac{1}{x} + \frac{2}{y + 1} = 1 \end{matrix}$ 时，如果设 $\frac{1}{x}$ ＝a ， $\frac{1}{y + 1}$ ＝b ，那么原方程组可化为二元一次方程组．

查看试题解析
12. 如果一个二元二次方程的一个解是 ${\begin{matrix} x = 2 \\ y = 4 \end{matrix}$ ，那么这个二元二次方程可以是．（只需写一个）

查看试题解析
13. 疫情期间，某快递公司推出无接触配送服务，第一周的订单数是5万件，第三周的订单数比第一周增加2.8万件，如果设平均每周订单数的增长率为x ，那么正确的方程是．

查看试题解析
14. 在△ABC中，如果 $\vec{A B}$ ＝ $\vec{a}$ ， $\vec{B C}$ ＝ $\vec{b}$ ，那么向量 $\vec{C A}$ ＝．（用向量 $\vec{a}$ 、 $\vec{b}$ 表示）

查看试题解析
15. 如图，∠1，∠2，∠3，∠4是五边形ABCDE的外角，且∠1＝∠2＝∠3＝∠4＝70°，则∠AED的度数是．

查看试题解析
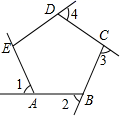16. 如果一个平行四边形周长是30cm，每一组邻边相差5cm，那么较长的边长是 cm．

查看试题解析
17. 如图，在矩形ABCD中，AB＝2AD＝2，E是边DC的中点，联结AE ．如果将△ADE沿AE所在的直线翻折，点D落在点F处，那么DF两点间的距离是．

查看试题解析
18. 我们定义：联结平行四边形一组对边中点的线段叫做“对边中位线”，联结平行四边形一组邻边中点的线段叫做“邻边中位线”．如图，在菱形ABCD中，∠A＝60°，对角线BD＝8，那么“对边中位线”EF与“邻边中位线”EG、FG所围成的△EFG的面积是．

查看试题解析

三、解答题

19. 下面是小明同学解无理方程3﹣ $\sqrt{2 x - 3}$ ＝x的过程：
原方程可变形为3﹣x＝ $\sqrt{2 x - 3}$ ……（第一步）

两边平方，得3﹣x＝2x﹣3……（第二步）

整理，得﹣3x＝6……（第三步）

解得x＝2……（第四步）

检验：把x＝2分别代入原方程的两边，左边＝3﹣ $\sqrt{2 x - 3}$ ＝2，右边＝2，左边＝右边，可知x＝2是原方程的解．……（第五步）

所以，原方程的解是x＝2．……（第六步）

请阅读上述小明的解题过程，并完成下列问题：

(1)、以上小明的解题过程中，从第步开始出错；

(2)、请完成正确求解方程3﹣ $\sqrt{2 x - 3}$ ＝x的过程．

查看试题解析
20. 解方程： $\frac{x + 1}{x - 1} - \frac{2}{x^{2} - 1} = \frac{1}{x + 1}$

查看试题解析
21. 根据医学上的科学研究表明，人在运动时的心跳的快慢通常与年龄有关．在正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数y（次）是这个人的年龄x（岁）的一次函数，年龄15岁和45岁的人在运动时所能承受的每分钟心跳的最高次数分别是164次和144次．

(1)、求y与x之间的函数关系式；（不需要写出定义域）

(2)、如果张伯伯今年54岁，他在一次跑步锻炼时，途中测得10秒心跳为24次，那么他此次的状况为 ▲ ．（请填“可能有危险”或“没有危险”），请通过计算说明理由．

查看试题解析
22. 木盒里有红球和白球，共4个，每个球除了颜色外其他都相同．从盒子里先摸出一个球，放回去摇匀后，再摸出一个球，继续放回去摇匀后，再摸第3次、第4次……

(1)、甲同学摸球10次，都没有摸到红球，于是他就判断“摸到红球”是“不可能事件”．他的判断符合题意吗？

(2)、如果盒子里有3个红球、1个白球，乙同学按照摸球的规则，摸球2次，那么摸到一个红球和1个白球的概率是多少？（用树状图展现所有等可能的结果）

查看试题解析
23. 已知梯形ABCD ， AB∥CD ， AD＝4，AB＝7．

(1)、如图1，联结BD ，当∠A＝60°时，求BD的长；

(2)、如图2，当∠D＝2∠B时，求CD的长．

查看试题解析
24. 已知：如图，四边形ABCD是菱形，点E ， F分别在边BC ， CD上，且BE＝DF ，过点F作AE的平行线交对角线AC的延长线于点G ，联结EG ．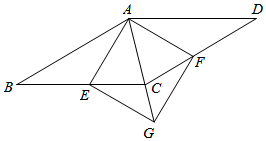

(1)、求证：四边形AEGF是菱形；

(2)、如果∠B＝∠BAE＝30°，求证：四边形AEGF是正方形．

查看试题解析
25. 在平面直角坐标平面xOy中（如图），已知直线y＝﹣x+m与直线y＝2x+n都经过点A（2，0），且分别与y轴交于点B和点C ．

(1)、求B、C两点的坐标；

(2)、设D是直角坐标平面内一点，如果以A、B、C、D为顶点的四边形是平行四边形，且AB是这个平行四边形的边，求点D的坐标．

查看试题解析
26. 如图，已知正方形ABCD的边长为1，点E ， F分别在边AB、AD上，且AE＝DF ．联结BF、CE ．

(1)、求证：BF＝CE；

(2)、如果将线段CE绕点E逆时针旋转90°，使得点C落在点G处，联结FG ．设AE＝x ．
①试用含x的代数式表示四边形BFGE的面积；

②当AF和EG互相平分时，求x的值．

查看试题解析