上海市崇明区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-15 类型：期末考试

进入出卷网下载

一、单选题

1. 一次函数 $y = - 5 x + 3$ 的图象不经过（）．

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列方程中，有实数根的方程是（）

A、 $x^{4} + 16 = 0$ B、 $x^{2} + 2 x + 3 = 0$ C、 $\sqrt{x} + \sqrt{x - 1} = 0$ D、 $\frac{x^{2} - 8}{x - 3} = \frac{1}{x - 3}$

查看试题解析
3. 将只有颜色不同的3个白球、2个黑球放在一个不透明的布袋中，下列四个选项，错误的是（）

A、摸到白球和黑球的可能性相等 B、摸到白球比摸到黑球的可能性大 C、摸到红球是不可能事件 D、摸到黑球或白球是确定事件

查看试题解析
4. 已知四边形 $A B C D$ 是矩形，点 $O$ 是对角线 $A C$ 与 $B D$ 的交点.下列四种说法：①向量 $\vec{A O}$ 与向量 $\vec{O C}$ 是相等的向量；②向量 $\vec{O A}$ 与向量 $\vec{O C}$ 是互为相反的向量；③向量 $\vec{A B}$ 与向量 $\vec{C D}$ 是相等的向量；④向量 $\vec{B O}$ 与向量 $\vec{B D}$ 是平行向量．其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 下列四个命题中，真命题是（）

A、对角线互相垂直的平行四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线相等的平行四边形是菱形 D、对角线相等的菱形是正方形

查看试题解析
6. 小张、小王两个人从甲地出发，去8千米外的乙地，图中线段OA、PB分别反映了小张、小王步行所走的路程S（千米）与时间t（分钟）的函数关系，根据图像提供的信息，小王比小张早到乙地的时间是__________分钟．

A、4 B、6 C、16 D、10

查看试题解析

二、填空题

7. 在直角坐标平面内，一次函数 $y = 2 x + 3$ 的图像在y轴上的截距是．

查看试题解析
8. 方程 $2 x^{3} - 16 = 0$ 的解是．

查看试题解析
9. 方程 $\sqrt{2 x - 3}$ =1的解是．

查看试题解析
10. 已知点 $A (- 2 ， a)$ 和点 $B (3 ， b)$ 在函数 $y = - 6 x + m$ 的图像上，那ab（填“＞”、“＝”或“ $=$ ”）．

查看试题解析
11. 已知一次函数 $y = k x + b$ 的图像经过点 $(- 3 ， 0)$ 与 $(0 ， 2)$ ，那么关于x的不等式 $k x + b > 0$ 的解集是．

查看试题解析
12. 用换元法解方程 $\frac{x}{x^{2} - 1} + \frac{2 (x^{2} - 1)}{x} = 4$ ，若设 $\frac{x}{x^{2} - 1} = y$ ，那么所得到的关于y的整式方程为．

查看试题解析
13. 如果从方程① $x + 1 = 0$ ，② $x^{2} - 2 x - 1 = 0$ ，③ $x + \frac{1}{x} = 1$ ，④ $\sqrt{x + 1} = 0$ ，⑤ $x^{4} - 1 = 0$ ，⑥ $\sqrt{x} + \frac{1}{\sqrt{x}} = 3$ 中任意选取一个方程，那么取到的方程是无理方程的概率是．

查看试题解析
14. 一个正多边形的每个内角度数均为135°，则它的边数为.

查看试题解析
15. 已知菱形的边长为2cm，一个内角为 $60 °$ ，那么该菱形的面积为cm² ．

查看试题解析
16. 已知一个梯形的中位线长为5 $c m$ ，其中一条底边的长为6 $c m$ ，那么该梯形的另一条底边的长是 $c m$ ．

查看试题解析
17. 当一个凸四边形的一条对角线把原四边形分割成两个等腰三角形时，我们称这个四边形为“等腰四边形”，其中这条对角线称为这个四边形的“等腰线”．如果凸四边形ABCD是“等腰四边形”，对角线AC是该四边形的“等腰线”，其中 $∠ B C D = 80 °$ ， $A B = B C = C D \neq A D$ ，那么 $∠ B A D$ 的度数为．

查看试题解析
18. 如图，在平面直角坐标系xOy中，直线 $y = 2 x - 1$ 分别与x轴、y轴交于点A、B ， $∠ A B C = 45 °$ ，那么直线BC的表达式是．

查看试题解析

三、解答题

19. 解方程： $\frac{x - 5}{x^{2} - 1} + 1 = \frac{3}{x + 1}$ ．

查看试题解析
20. 解方程组： ${\begin{array}{l} x + 2 y = 3 \\ x^{2} - 4 x y + 4 y^{2} = 1 \end{array}$ ．

查看试题解析
21.

(1)、已知四边形OBCA是平行四边形，点D在OB上．

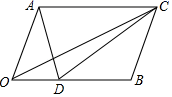
①填空： $\vec{O A} + \vec{A C} =$ ▲ ； $\vec{A D} - \vec{O B} =$ ▲ ；

②求作： $\vec{O A} + \vec{C O} - \vec{C B}$ ．

(2)、在一个不透明的袋子中装有（除颜色外）完全相同的红色小球1个，白色小球1个和黄色小球2个．
①如果从中先摸出一个小球，记下它的颜色后，将他放回袋子中摇匀，再摸出一个小球，记录下颜色，那么摸出的两个小球的颜色恰好是“一红一黄”的概率是；

②如果摸出的第一个小球之后不放回袋子中，再摸出第二个小球，这时摸出的两个小球的颜色恰好是“一红一黄”的概率是．

查看试题解析
22. 某西红花种植基地需要种植5000株西红花．最初采用人工种植，种植了2000株后，为提高效率，采用机械化种植，机械化种植比人工种植每小时多种植50株，结果比原计划提前30小时完成任务．求人工种植每小时种多少株西红花？

查看试题解析
23. 如图，在 $△ A C B$ 中， $∠ A B C = 90 °$ ，点D是斜边AC上的一点， $D A = D B$ ，点F是AB的中点，过点C作 $C E / / B D$ 交FD的延长线于点E ．

(1)、求证：四边形CBDE是平行四边形；

(2)、联结BE、AE ，如果 $∠ C B E = 45 °$ ，求证： $A B = 3 B C$ ．

查看试题解析
24. 在平面直角坐标系xOy中，已知直线 $y = - \frac{1}{2} x + 2$ 分别与x轴、y轴交于点A、B ，直线 $y = k x - 1$ 的图像与y轴交于点C ，与已知直线交于点D ，点D的横坐标是2

(1)、求直线 $y = k x - 1$ 的解析式；

(2)、将直线 $y = k x - 1$ 的图像向上或向下平移，交直线 $y = - \frac{1}{2} x + 2$ 于点E ，设平移所得函数图象的截距为b ，如果交点E始终落在线段AB上，求b的取值范围．

(3)、在x轴上是否存在点P ，使点P与点A、B、C构成的四边形为梯形，如果存在，请求出点P的坐标；如果不存在，请说明理由．

查看试题解析
25. 实践操作：

第一步：如图1，将矩形纸片ABCD沿过点D的直线折叠，使点A落在CD上的点 $A^{'}$ 处，得到折痕DE ，然后把纸片展平；

第二步：如图2，将图1中的矩形纸片ABCD沿过点E的直线折叠，点C恰好落在AD上的点 $C^{'}$ 处，点 $B$ 落在点 $B^{'}$ 处，得到折痕EF ， $B^{'} C^{'}$ 交AB于点M ， $C^{'} F$ 交DE于点N ，再把纸片展平．

问题解决：

(1)、如图1，填空：四边形 $A E A^{'} D$ 的形状是；

(2)、如图2，线段 $M C^{'}$ 与ME是否相等？若相等，请给出证明；若不等，请说明理由；

(3)、如图2，若 $A C^{'} = 2 cm$ ， $D C^{'} = 4 cm$ ，求线段DF的长．

查看试题解析