上海市宝山区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，无理方程是（）

A、 $\sqrt{5} x - 1 = 0$ B、 $\sqrt{x + 1} = x$ C、 $\frac{x}{\sqrt{2} - x} = 1$ D、 $\frac{x^{2} - 1}{x + 1} = 1$

查看试题解析
2. 下列关于x的方程中，一定有实数根的是（）

A、 $a x - 1 = 0$ B、 $a^{2} x - 1 = 0$ C、 $x^{2} - a = 0$ D、 $x^{3} - a = 0$

查看试题解析
3. 下列关于向量的等式中，正确的是（）

A、 $\vec{A B} + \vec{B C} = \vec{C B} + \vec{B A}$ B、 $\vec{A B} + \vec{B C} + \vec{C D} = \vec{D A}$ C、 $\vec{A B} + \vec{B C} + \vec{C A} = \vec{0}$ D、 $\vec{A B} - \vec{B C} = \vec{A C}$

查看试题解析
4. 下列四边形中，对角线相等且互相平分的是（）

A、平行四边形 B、菱形 C、矩形 D、等腰梯形

查看试题解析
5. 下列事件中，确定事件是（）

A、车辆随机到达一个路口，遇到红灯 B、明天要下图 C、掷一枚质地均匀的硬币，正面朝上 D、明天太阳从西边升起

查看试题解析
6. 四边形不具稳定性，四条边长都确定的四边形．当内角的大小发生变化时．其形状也随之改变．如图，改变正方形 $A B C D$ 的内角，使正方形 $A B C D$ 变为菱形 $A B C^{'} D^{'}$ ，如果 $∠ D A D^{'} = 30 °$ ，那么菱形 $A B C^{'} D^{'}$ 与正方形 $A B C D$ 的面积之比是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看试题解析

二、填空题

7. 一次函数 $y = - \sqrt{2} x - 1$ 的图像在y轴上的截距是．

查看试题解析
8. 已知一次函数 $f (x) = \frac{1}{2} x - 1$ ，如果 $f (a) = 3$ ，那么实数a的值为．

查看试题解析
9. 已知一次函数 $y = k x + b (k \neq 0)$ 的图像如图所示，那么不等式 $k x + b > 0$ 的解集是．

查看试题解析
10. 方程 $x^{3} - 8 = 0$ 的根是．

查看试题解析
11. 已知关于x的方程 $\frac{x}{x^{2} - 1} - \frac{x^{2} - 1}{x} = 1$ ，如果设 $\frac{x}{x^{2} - 1} = y$ ，那么原方程可化为关于y的整式方程是．

查看试题解析
12. 数学家斐波那契编写的《算经》中有如下问题：一组人平分10元钱，每人分得若干；若再加上6人，平分40元钱，则第二次每人所得与第一次相同，求第一次分钱的人数，设第一次分钱的人数为x人，则可列方程。

查看试题解析
13. 不透明的布袋里有3个小球分别标有数字1、2、3，它们除所标数字外其它都相同．如果任意摸出一个小球记下所标数字后，将该小球放回袋中，搅匀后再摸出一个小球，那么两次摸到的小球所标数字的和能被2整除的概率是．

查看试题解析
14. 如果多边形的每个外角都是 $72 °$ ，那么这个多边形的边数是．

查看试题解析
15. 如图，已知 $▱ A B C D$ 中， $A B = 4 ， A D = 7$ ．如果作 $∠ A B C$ 与 $∠ B C D$ 的平分线分别交 $A D$ 于点E、F ，那么 $E F$ 的长是．

查看试题解析
16. 如图，已知 $▱ A B C D$ 中， $A B = 6 ， A D = 8 ， A H ⊥ B C$ ，垂足为点H ，点M、N分别是 $A H$ 、 $C D$ 的中点．联结 $M N$ ．如果 $M N = 6.5$ ，那么 $∠ C$ 的度数是．

查看试题解析
17. 如图，在梯形 $A B C D$ 中， $A D // B C ， A B ⊥ B C$ ．已知 $A D = 3 ， C D = 5 ， B C = 2 A D$ ．点E是 $A B$ 边上的中点，联结 $D E$ ，那么 $D E$ 的长是．

查看试题解析
18. 如图，将平行四边形纸片 $A B C D$ 沿一条直线折叠，使点A与点C重合，点D落在点G处，折痕为 $E F$ ．已知 $B C = 4 ， B E = 2 ， ∠ B = 60 °$ ，那么 $△ F C G$ 的面积为．

查看试题解析

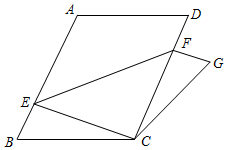
三、解答题

19. 解方程： $\sqrt{3 x + 6} - \sqrt{x + 3} = 1$ ．

查看试题解析
20. 解方程组： ${\begin{array}{l} x = 3 y + 2 ， \\ x^{2} - 2 x y + y^{2} - 16 = 0. \end{array}$

查看试题解析
21. 如图，在梯形 $A B C D$ 中， $A D // B C$ ，已知 $\vec{A B} = \vec{a} ， \vec{B C} = \vec{b} ， \vec{A D} = \vec{c}$ ．

(1)、试用向量 $\vec{a}$ 、 $\vec{b}$ 、 $\vec{c}$ 表示下列向量： $\vec{A C} =$ ， $\vec{D C} =$ ；

(2)、求作： $\vec{A B} - \vec{A D}$ 、 $\vec{A B} + \vec{A D}$ ．（不要求写作法，要写明结论）

查看试题解析
22. 甲，乙两名摩托车选手在匀速状态下进行赛道训练，已知两名选手先后从起点A地驶往相距60千米的终点B地．如果甲的速度比乙的速度慢1千米/分钟．甲比乙早出发1分钟，最后乙先到达终点B地．设甲的行驶时间为x（分钟），甲、乙的行驶路程 $y_{甲}$ 、 $y_{乙}$ （千米）与x之间的函数图象如图所示．

(1)、根据图像，回答问题：
当乙到达终点B地时， $y_{甲} =$ 千米；

(2)、求甲、乙两名摩托车选手的速度；

(3)、求 $y_{乙}$ 关于x的函数解析式．

查看试题解析
23. 如图，已知菱形 $A B C D$ 中， $∠ B = 60 °$ ，点E、F分别在边 $B C$ 、 $C D$ 上，且 $∠ E A F = 60 °$ ，联结 $E F$ ．

(1)、求证： $△ A E F$ 是等边三角形；

(2)、当 $A B = 2$ 时，求 $△ A E F$ 周长的最小值．

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，已知点C的坐标为 $(3 ， 1)$

(1)、求直线 $O C$ 的表达式；

(2)、以线段 $O C$ 为边作正方形 $O A B C$ ，点A、B在直线 $O C$ 的下方，求点A的坐标；

(3)、设直线 $C A$ 与y轴交于点E ，点F在y轴右侧，且 $△ O A E$ 与 $△ O C F$ 全等，顶点O、A、E分别与顶点O、C、F对应，求 $E F$ 的长．

查看试题解析
25. 将两张宽度相等的纸片叠放在一起，得到如图的四边形 $A B C D$ ．

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、如图，联结 $A C$ ，过点A、D分别作 $B C$ 的垂线 $A F$ 、 $D E$ ，垂足分别为点F、E ．
①设M为 $A C$ 中点，联结 $E M$ 、 $F M$ ，求证： $E M ⊥ F M$ ；

②如果 $A F = 3 F C$ ，P是线段 $A C$ 上一点（不与点A、C重合），当 $△ A P F$ 为等腰三角形时，求 $\frac{S_{△ A P F}}{S_{四边形 A B C D}}$ 的值．

查看试题解析