广东省汕头市龙湖区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 下列式子中,属于最简二次根式的是A、 B、 C、 D、2. 下列各组数中,不能构成直角三角形的一组是( )A、3,4,5 B、1,2, C、5,12,13 D、6,8,123. 下列计算正确的是( )A、 B、 C、 D、4. 数据3、4、6、7、x的平均数是5,这组数据的中位数是( )A、4 B、4.5 C、5 D、65. 如图在▱ABCD中,已知AC=4cm,若△ACD的周长为13cm,则▱ABCD的周长为( )
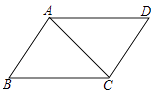 A、26cm B、24cm C、20cm D、18cm6. 我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是x尺.根据题意,可列方程为( )
A、26cm B、24cm C、20cm D、18cm6. 我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是x尺.根据题意,可列方程为( ) A、 B、 C、 D、7. 对于函数 ,下列结论正确的是( )A、它的图象必经过点(-1,1) B、它的图象不经过第三象限 C、当 时, D、 的值随 值的增大而增大8. 菱形具有而一般平行四边形不具有的性质是( )A、对边相等 B、对角相等 C、对角线互相平分 D、对角线互相垂直9. 在平面直角坐标系中,一次函数 的图象是( )A、
A、 B、 C、 D、7. 对于函数 ,下列结论正确的是( )A、它的图象必经过点(-1,1) B、它的图象不经过第三象限 C、当 时, D、 的值随 值的增大而增大8. 菱形具有而一般平行四边形不具有的性质是( )A、对边相等 B、对角相等 C、对角线互相平分 D、对角线互相垂直9. 在平面直角坐标系中,一次函数 的图象是( )A、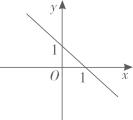 B、
B、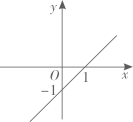 C、
C、 D、
D、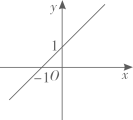 10. 如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),D对角线AC、BD相交于点O , 过点P分别作AC、BD的垂线,分别交AC、BD于点E、F , 交AD、BC于点M、N . 下列结论:①ΔAPE≌ΔAME;②PM+PN=AC;③PE2+PF2=PO2;④BN= PF . 其中正确结论的有( )个.
10. 如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),D对角线AC、BD相交于点O , 过点P分别作AC、BD的垂线,分别交AC、BD于点E、F , 交AD、BC于点M、N . 下列结论:①ΔAPE≌ΔAME;②PM+PN=AC;③PE2+PF2=PO2;④BN= PF . 其中正确结论的有( )个.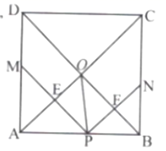 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
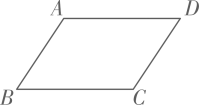
11. 二次根式 有意义,则 的取值范围是 .12. 如图,在四边形ABCD中,已知AB=CD,再添加一个条件(写出一个即可,图形中不再添加助线),则四边形ABCD是平行四边形.
 13. 在一次函数 中, 随 的增大而减小,则 的取值范围是 .14. 现有甲、乙两个合唱队,队员的平均身高都是175cm,方差分别为 =0.51, =0.35,那么两个队中队员的身高较整齐的是队.(填“甲”、“乙”中的一个)15. 如图,已知直线y=ax+b和直线y=kx交于点P , 若二元一次方程组 的解为x、y , 则关于x+y= .
13. 在一次函数 中, 随 的增大而减小,则 的取值范围是 .14. 现有甲、乙两个合唱队,队员的平均身高都是175cm,方差分别为 =0.51, =0.35,那么两个队中队员的身高较整齐的是队.(填“甲”、“乙”中的一个)15. 如图,已知直线y=ax+b和直线y=kx交于点P , 若二元一次方程组 的解为x、y , 则关于x+y= .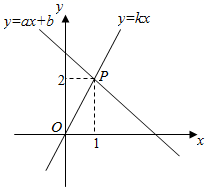 16. 如图,菱形ABCD的边长为4,∠A=45°,分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧相交于M , N两点,直线MN交AD于点E , 连接CE , 则CE的长为 .
16. 如图,菱形ABCD的边长为4,∠A=45°,分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧相交于M , N两点,直线MN交AD于点E , 连接CE , 则CE的长为 .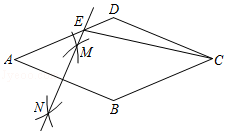 17. 如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1 , 以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2 , 交x轴于点B2 , 以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3 , 交直线l于点D3 , 以A3D3为边作正方形A3B3C3D3 , ……依此类推,则正方形A2B2C2D2的面积为;正方形AnBnCnDn的面积为 .
17. 如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1 , 以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2 , 交x轴于点B2 , 以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3 , 交直线l于点D3 , 以A3D3为边作正方形A3B3C3D3 , ……依此类推,则正方形A2B2C2D2的面积为;正方形AnBnCnDn的面积为 .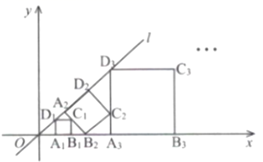
三、解答题
-
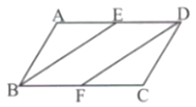
18. 计算: .19. 如图,在平行四边形ABCD中,E , F分别是AD , BC的中点.求证:BE=DF .
 20. 已知一次函数的图象经过点(2,1)和(0,-2).(1)、求该函数的解析式;(2)、判断点(-4,6)是否在该函数图象上.21. 在开展“学雷锋社会实践”活动中,某校为了解全校1000名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成如图的条形统计图:
20. 已知一次函数的图象经过点(2,1)和(0,-2).(1)、求该函数的解析式;(2)、判断点(-4,6)是否在该函数图象上.21. 在开展“学雷锋社会实践”活动中,某校为了解全校1000名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成如图的条形统计图: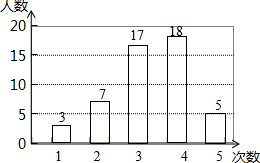 (1)、这50个样本数据的中位数是次,众数是次;(2)、求这50个样本数据的平均数;(3)、根据样本数据,估算该校1000名学生大约有多少人参加了4次实践活动.22. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD , BC交于M , N两点,连接CM , AN .
(1)、这50个样本数据的中位数是次,众数是次;(2)、求这50个样本数据的平均数;(3)、根据样本数据,估算该校1000名学生大约有多少人参加了4次实践活动.22. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD , BC交于M , N两点,连接CM , AN .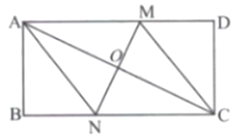 (1)、求证:四边形ANCM为平行四边形;(2)、若AD=4,AB=2,且MN⊥AC , 求DM的长.23. 某工厂计划生产A、B两种产品共50件,已知A产品成本2000元/件,售价2300元/件;B种产品成本3000元/件,售价3500元/件,设该厂每天生产A种产品x件,两种产品全部售出后共可获利y元.(1)、求出y与x的函数表达式;(2)、如果该厂每天最多投入成本140000元,那么该厂生产的两种产品全部售出后最多能获利多少元?24.
(1)、求证:四边形ANCM为平行四边形;(2)、若AD=4,AB=2,且MN⊥AC , 求DM的长.23. 某工厂计划生产A、B两种产品共50件,已知A产品成本2000元/件,售价2300元/件;B种产品成本3000元/件,售价3500元/件,设该厂每天生产A种产品x件,两种产品全部售出后共可获利y元.(1)、求出y与x的函数表达式;(2)、如果该厂每天最多投入成本140000元,那么该厂生产的两种产品全部售出后最多能获利多少元?24.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
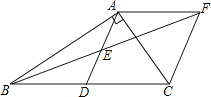 (1)、求证:△AEF≌△DEB
(1)、求证:△AEF≌△DEB
(2)、证明四边形ADCF是菱形。
(3)、若AC=4,AB=5,求菱形ADCF的面积.25. 如图,在平面直角坐标系中,函数y=-x+2的图象与x轴,y轴分别交于点A , B , 与函数y= x+b的图象交于点C(-2,m).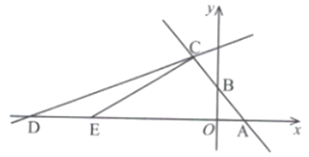 (1)、求m和b的值;(2)、函数y=x+b的图象与x轴交于点D , 点E从点D出发沿DA向,以每秒2个单位长度匀速运动到点M(到A停止运动),设点E的运动时间为1秒.
(1)、求m和b的值;(2)、函数y=x+b的图象与x轴交于点D , 点E从点D出发沿DA向,以每秒2个单位长度匀速运动到点M(到A停止运动),设点E的运动时间为1秒.①当ΔACE的面积为12时,求t的值;
②在点E运动过程中,是否存在t的值,使ΔACE为直角三角形?若存在,请求出t的值;若不存在,请说明理由.