广东省广州市花都区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 若 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 下列各组数中,能构成直角三角形三边长的是( )A、2,2,3 B、3,4,5 C、4,5,6 D、1, ,34. 下列运算结果正确的是( )A、 B、 C、 D、5. 在一次中学生田径运动会上,参加女子立定跳远的15名运动员的成绩情况统计如下:
成绩(米)
1.50
1.60
1.65
1.70
1.75
人数(人)
2
3
2
5
3
则这15名运动员立定跳远成绩的众数与中位数分别是( )
A、1.70,1.70 B、1.70,1.65 C、1.65,1.65 D、1.65,1.706. 将直线 向上平移4个单位长度,所得直线的解析式是( )A、 B、 C、 D、7. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,则下列一定成立的是( ) A、 B、 C、 D、8. 如图,已知平行四边形 的对角线 , 相交于点 ,下列选项能使平行四边形 成为矩形的条件是( )
A、 B、 C、 D、8. 如图,已知平行四边形 的对角线 , 相交于点 ,下列选项能使平行四边形 成为矩形的条件是( ) A、 B、 C、 D、9. 如图,折线表示一骑车人离家的距离 与时间 的关系,骑车人9:00离开家,15:00回到家,则下列说法错误的是( )
A、 B、 C、 D、9. 如图,折线表示一骑车人离家的距离 与时间 的关系,骑车人9:00离开家,15:00回到家,则下列说法错误的是( )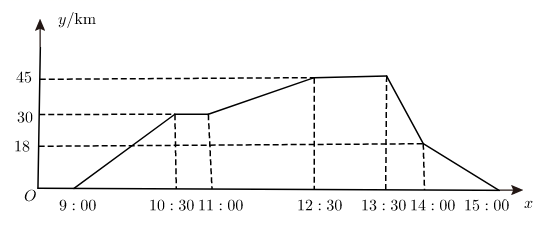 A、骑车人离家最远距离是45km B、骑车人中途休息的总时间长是1.5h C、从9:00到10:30骑车人离家的速度越来越大 D、骑车人返家的平均速度是30km/h10. 一次函数 与 在同一个平面直角坐标系中的图象可能是( )A、
A、骑车人离家最远距离是45km B、骑车人中途休息的总时间长是1.5h C、从9:00到10:30骑车人离家的速度越来越大 D、骑车人返家的平均速度是30km/h10. 一次函数 与 在同一个平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 计算:32=12. 甲、乙两个芭蕾舞团的女学员身高的方差分别是 、 ,则女学员身高更整齐的是芭蕾舞团(填“甲”或“乙”).13. 如图,在 中, , ,则 .
 14. 已知 ,则化简 .15. 已知一次函数 的图象如图所示,则关于 的不等式 的解集为 .
14. 已知 ,则化简 .15. 已知一次函数 的图象如图所示,则关于 的不等式 的解集为 . 16. 如图,正方形 的边长为6,点 、 分别在 、 上,点 为 的中点.将 , 分别沿 , 向内折叠,此时 与 重合( 、 都落在点 ),连接 .则下列结论正确的有(直接写序号即可)
16. 如图,正方形 的边长为6,点 、 分别在 、 上,点 为 的中点.将 , 分别沿 , 向内折叠,此时 与 重合( 、 都落在点 ),连接 .则下列结论正确的有(直接写序号即可)① ;② ;③三角形 是等边三角形; ④三角形 的面积为30.

三、解答题
-
17. 计算:18.
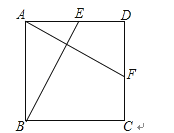
如图,正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
 19. 八年级(1)班的50名同学在一次班会课上进行了“百科知识”的答题竞赛.竞赛共有10道题,参赛的同学最多答对了10题,最少答对了6题.学习委员将同学们答对题数进行统计,并绘制成如下的统计图,请根据图表中提供的信息解答下列问题:
19. 八年级(1)班的50名同学在一次班会课上进行了“百科知识”的答题竞赛.竞赛共有10道题,参赛的同学最多答对了10题,最少答对了6题.学习委员将同学们答对题数进行统计,并绘制成如下的统计图,请根据图表中提供的信息解答下列问题: (1)、请补全条形图.(2)、请求出这50名同学答对题数的平均数.20. 如图,在四边形 中, , , , . ,求四边形 的面积.
(1)、请补全条形图.(2)、请求出这50名同学答对题数的平均数.20. 如图,在四边形 中, , , , . ,求四边形 的面积.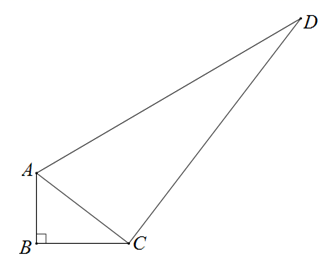 21. 学习完一次函数后,某班同学在数学老师的指导下,继续对函数 的图象和性质进行探究.同学们在研究的过程中发现,这个函数的自变量 的取值范围是全体实数,他们将 与 的几组对应值列表(如下表),并画出了函数图象的一部分(如图).
21. 学习完一次函数后,某班同学在数学老师的指导下,继续对函数 的图象和性质进行探究.同学们在研究的过程中发现,这个函数的自变量 的取值范围是全体实数,他们将 与 的几组对应值列表(如下表),并画出了函数图象的一部分(如图).…
0
1
2
3
4
5
…
…
3
2
1
0
1
2
3
4
…

请你完成以下的研究问题:
(1)、表中的 .(2)、根据上表的数据,画出函数图象的另一部分.(3)、请你根据函数 的图象判断以下两种说法(在相应的括号内填“对”或“错”).①当 时, 随 的增大而增大( )﹔
②函数图象一定经过点 ( ).
22. 如图,点 、 分别在矩形 的边上,将矩形 沿直线 向上折叠,使得点 落到点 的位置,点 落到点 的位置,连接 、 , 交 于点 . (1)、求证: 是等腰三角形;(2)、若 , ,求线段 的长.23. 为了满足开展“阳光体育”大课间活动的需求,某学校计划购买一批篮球.根据学校的规模,需购买 、 两种不同型号的篮球共300个.已知购买3个 型篮球和2个 型篮球共需340元,购买2个 型篮球和1个 型篮球共需要210元.(1)、求购买一个 型篮球、一个 型篮球各需多少元?(2)、若该校计划投入资金 元用于购买这两种篮球,设购进的 型篮球为 个,求 关于 的函数关系式;(3)、在(2)的条件下,若购买 型篮球的数量不超过 型篮球数量的2倍,则该校至少需要投入资金多少元?24. 阅读短文,解决问题
(1)、求证: 是等腰三角形;(2)、若 , ,求线段 的长.23. 为了满足开展“阳光体育”大课间活动的需求,某学校计划购买一批篮球.根据学校的规模,需购买 、 两种不同型号的篮球共300个.已知购买3个 型篮球和2个 型篮球共需340元,购买2个 型篮球和1个 型篮球共需要210元.(1)、求购买一个 型篮球、一个 型篮球各需多少元?(2)、若该校计划投入资金 元用于购买这两种篮球,设购进的 型篮球为 个,求 关于 的函数关系式;(3)、在(2)的条件下,若购买 型篮球的数量不超过 型篮球数量的2倍,则该校至少需要投入资金多少元?24. 阅读短文,解决问题定义:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”﹒例如:如图1,四边形 为菱形, 与 重合,点 在 上,则称菱形 为 的“亲密菱形”.
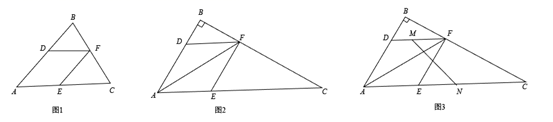
如图2,在 中, , 平分 ,交 于点 ,过点 作 , .
(1)、求证:四边形 为 的“亲密菱形”;(2)、若 , ,求四边形 的周长;(3)、如图3, 、 分别是 、 的中点,连接 .若 ,求 的值.25. 如图,直线 : 分别与 轴, 轴交于 , 两点,在 上取一点 ,以线段 为边向右作正方形 ,正方形 沿 的方向以每秒1个单位长度的速度向右作匀速运动,设运动时间为 秒 .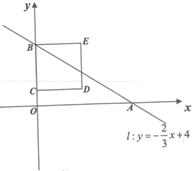 (1)、求 , 两点的坐标;(2)、在正方形 向右运动的过程中,若正方形 的顶点落在直线 上,求 的值;(3)、设正方形 两条对角线交于点 ,在正方形向右运动的过程中,是否存在实数 ,使得 有最小值?若存在,求出 的值:若不存在,请说明理由.
(1)、求 , 两点的坐标;(2)、在正方形 向右运动的过程中,若正方形 的顶点落在直线 上,求 的值;(3)、设正方形 两条对角线交于点 ,在正方形向右运动的过程中,是否存在实数 ,使得 有最小值?若存在,求出 的值:若不存在,请说明理由.