广东省广州市番禺区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 一次函数 的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限3. 如图,在▱ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数等于( )
 A、45° B、55° C、65° D、75°4. 下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )A、 , , B、1, ,2 C、3,6,9 D、4,5,65. 直线y=2x向下平移2个单位长度得到的直线是( )A、y=2(x+2) B、y=2(x﹣2) C、y=2x﹣2 D、y=2x+26. 如图,在 中, , 于 , 是边 的中点, ,则 的长为( )
A、45° B、55° C、65° D、75°4. 下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )A、 , , B、1, ,2 C、3,6,9 D、4,5,65. 直线y=2x向下平移2个单位长度得到的直线是( )A、y=2(x+2) B、y=2(x﹣2) C、y=2x﹣2 D、y=2x+26. 如图,在 中, , 于 , 是边 的中点, ,则 的长为( ) A、 B、 C、 D、7. 下列命题中是假命题的是( )A、对角线相等且互相平分的四边形是矩形; B、对角线相等的菱形是正方形; C、有一组邻边相等的平行四边形是菱形; D、一组对边平行,另一组对边相等的四边形是平行四边形.8. 有一组数据:2, ,4,6,7,它们的平均数是5,则这组数据的中位数是( )A、6 B、5 C、4 D、39. 如图,四边形OABC为矩形,点A的坐标为(0,2),点C的坐标为(4,0),若直线y=kx−k−1将矩形OABC分成面积相等的两部分,则k的值为( )
A、 B、 C、 D、7. 下列命题中是假命题的是( )A、对角线相等且互相平分的四边形是矩形; B、对角线相等的菱形是正方形; C、有一组邻边相等的平行四边形是菱形; D、一组对边平行,另一组对边相等的四边形是平行四边形.8. 有一组数据:2, ,4,6,7,它们的平均数是5,则这组数据的中位数是( )A、6 B、5 C、4 D、39. 如图,四边形OABC为矩形,点A的坐标为(0,2),点C的坐标为(4,0),若直线y=kx−k−1将矩形OABC分成面积相等的两部分,则k的值为( ) A、 B、 C、2 D、10. 如图,矩形 中, 为 的中点,过点 的直线分别与 , 交于点 , ,连接 交 于点 ,连接 , .若 , ,则下列结论:
A、 B、 C、2 D、10. 如图,矩形 中, 为 的中点,过点 的直线分别与 , 交于点 , ,连接 交 于点 ,连接 , .若 , ,则下列结论:
① ;② ;③四边形 是菱形;④ .
其中正确结论的个数是( )
A、4 B、3 C、2 D、1二、填空题
-
11. 代数式 有意义时,实数 的取值范围是12. 计算: .13. 已知直角三角形两边的长分别是3和4,则第三边的长为 .14. 在8年级运动会的投飞镖比赛中,7名同学的投掷成绩(单位:环)分别是:7,9,9,4,9,8,8,这组数据的众数是 .15. 在平面直角坐标系中,已知一次函数 的图象经过 , 两点,若 ,则 .(填“>”“<”“=”)16. 如图,在平面直角坐标系中, 的边 在 轴上,且 ,点 的坐标为 点 为 的中点, 的垂直平分线交 轴于点 ,交 于点 ,点 为线段 上的一动点,当 的周长最小时,点 的坐标为 .

三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 如图,在 中, , , ,将 折叠,使点 恰好落在斜边 上,与点 重合, 为折痕,求 和 的长.
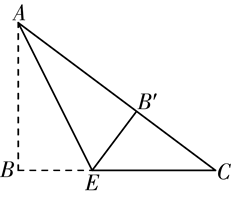 19. 如图,四边形 是正方形, 是 上的任意一点, 于点 , ,且交 于点 .
19. 如图,四边形 是正方形, 是 上的任意一点, 于点 , ,且交 于点 .求证: .
 20. 某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛,现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录,甲、乙、丙三个小组各项得分如下表:
20. 某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛,现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录,甲、乙、丙三个小组各项得分如下表:小组
研究报告
小组展示
答辩
甲
91
80
78
乙
81
74
85
丙
79
83
90
(1)、计算各小组平均成绩;(2)、如果按照研究报告占40%,小组展示占30%,答辩占30%,计算各小组成绩,哪个小组的成绩最高?21. 如图, , 分别是菱形 的边 , 的中点,且 , . (1)、求线段 的长;(2)、探究四边形 是什么特殊四边形?并对结论给予证明.22. 已知,一次函数y=kx+b的图象经过M(−1,1),N(1,5)两点.(1)、求一次函数的解析式;(2)、当 取何值时, ?23. 一种千斤顶利用了四边形的不稳定性.如图为一个水平放置的千斤顶,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变 的大小(菱形的边长不变),从而改变千斤顶的高度(即 、 之间的距离).若 ,当 从 变为 时,千斤顶升高了多少?( , ,结果保留整数)
(1)、求线段 的长;(2)、探究四边形 是什么特殊四边形?并对结论给予证明.22. 已知,一次函数y=kx+b的图象经过M(−1,1),N(1,5)两点.(1)、求一次函数的解析式;(2)、当 取何值时, ?23. 一种千斤顶利用了四边形的不稳定性.如图为一个水平放置的千斤顶,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变 的大小(菱形的边长不变),从而改变千斤顶的高度(即 、 之间的距离).若 ,当 从 变为 时,千斤顶升高了多少?( , ,结果保留整数)

