安徽省合肥市高新区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 用配方法解 方程,将其化成 的形式,则变形正确的是( )A、 B、 C、 D、4. 若一个多边形的所有内角与外角的和是 ,则该多边形的边数为( )A、6 B、7 C、8 D、95. 若 ,则 的值为( )A、4 B、-4 C、-1 D、4或-16. 要使平行四边形 成为矩形,需要添加的条件是( )A、 B、 C、 D、7. 下列命题中,是假命题的是( )A、在 中,若 、则 是直角三角形 B、在 中,若 ,则 是直角三角形 C、在 中,若 ,则 是直角三角形 D、在 中,若 ,则 是直角三角形8. 小梅每天坚持背诵英语单词,她记录了某一周每天背诵英语单词的个数,如下表:
星期
日
一
二
三
四
五
六
个数
11
12
13
10
13
13
其中有一天的个数被墨汁覆盖了,但小梅已经计算出这组数据唯一众数是13,平均数12,那么这组数据的方差是( )
A、 B、 C、1 D、9. 随着美丽乡村建设和发展,某乡村2019年旅游总收入为a万元,计划到2021年旅游总收入在2019年基础上翻两番.设每年的旅游总收入平均增长率为x,以下方程正确的是( )A、 B、 C、 D、10. 如图,在 中, 两顶点 在 轴、 轴上滑动,点 在第一象限内,连接 ,则 的最大值为( )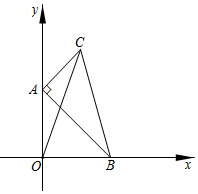 A、7 B、8 C、9 D、
A、7 B、8 C、9 D、二、填空题
-
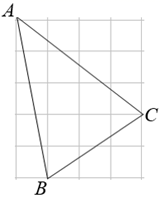
11. .12. 关于x的一元二次方程 的一个根是 ,则这个方程的另一根为 .13. 如图,在正方形网格中,每个小正方形的边长为 是网格上的格点三角形,则它的边 上的高等于 .
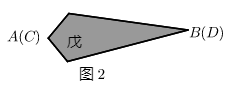
 14. 如图1,平行四边形纸片 的面积为 .今沿两对角线将四边形 剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并( 重合)形成一个对称图形戊,如图2所示.则图形戊的两条对角线长度之和为 .
14. 如图1,平行四边形纸片 的面积为 .今沿两对角线将四边形 剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并( 重合)形成一个对称图形戊,如图2所示.则图形戊的两条对角线长度之和为 .
 15. 如图,矩形 中,对角线 交于点 于 ,若 .则 的值为 .
15. 如图,矩形 中,对角线 交于点 于 ,若 .则 的值为 .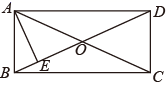
三、解答题
-
16.(1)、计算:(2)、解方程: (2 x -1)( x + 3) = 417. 定义新运算,对干任意实数 .都有 .例如: .若 的值小于 .请判断方程: 的根的情况.18. 如图,四边形 是菱形,对角线 相交于点 ,点 是边 上一点,连接 ,若 ,求 的长.
 19. 某校八年级在一次体育模拟测试中,随机抽查了部分学生的体育成绩(满分为70分),根据成绩分成如下六组 .并根据数据制作出如下不完整的统计图.请根据统计图解决下列问题:
19. 某校八年级在一次体育模拟测试中,随机抽查了部分学生的体育成绩(满分为70分),根据成绩分成如下六组 .并根据数据制作出如下不完整的统计图.请根据统计图解决下列问题: (1)、补全频数分布直方图,并求出 的值;(2)、本次体育模拟测试成绩的中位数落在哪一组?(3)、该校八年级有500名学生,且都参加了这次模拟测试,若测试成绩不低于60分为优秀,则该校八年级成绩优秀的学生约有多少人?20. 如图,点 是 内一点,连接 并将 的中点 、G依次连接.得到四边形 .
(1)、补全频数分布直方图,并求出 的值;(2)、本次体育模拟测试成绩的中位数落在哪一组?(3)、该校八年级有500名学生,且都参加了这次模拟测试,若测试成绩不低于60分为优秀,则该校八年级成绩优秀的学生约有多少人?20. 如图,点 是 内一点,连接 并将 的中点 、G依次连接.得到四边形 .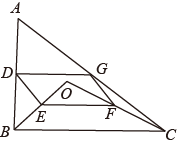 (1)、求证:四边形 是平行四边形;(2)、如果 ,求 的长.21. 超市销售某种儿童玩具,经市场调查发现,每件利润为 元时,每天可售出 件;销售单价每增加 元,每天销售量会减少 件.物价管理部门规定,该种玩具每件利润不得超过 元.设销售单价增加 元,每天可售出 件.(1)、写出 与 之间的函数关系式(不要求写出自变量取值范围);(2)、当 取何值时,超市每天销售这种玩具可获得利润 元?此时每天可销售多少件?22. 如图,正方形 ABCD 中 ,点E在边CD上,且CD=3DE .将 △ADE 沿 AE 翻折至 △AFE ,延长 EF 交边 BC 于点 G ,连结 AG、CF .
(1)、求证:四边形 是平行四边形;(2)、如果 ,求 的长.21. 超市销售某种儿童玩具,经市场调查发现,每件利润为 元时,每天可售出 件;销售单价每增加 元,每天销售量会减少 件.物价管理部门规定,该种玩具每件利润不得超过 元.设销售单价增加 元,每天可售出 件.(1)、写出 与 之间的函数关系式(不要求写出自变量取值范围);(2)、当 取何值时,超市每天销售这种玩具可获得利润 元?此时每天可销售多少件?22. 如图,正方形 ABCD 中 ,点E在边CD上,且CD=3DE .将 △ADE 沿 AE 翻折至 △AFE ,延长 EF 交边 BC 于点 G ,连结 AG、CF . (1)、求 的度数;(2)、求证: ;(3)、若 ,则 的面积等于 .
(1)、求 的度数;(2)、求证: ;(3)、若 ,则 的面积等于 .