安徽省阜阳市颍州区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-15 类型：期末考试

进入出卷网下载

一、单选题

1. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是（）

A、x≤3 B、x＜3 C、x≥3 D、x＞3

查看试题解析
2. 若一次函数y=ax＋b的图象经过第一、二、四象限，则下列不等式成立的是（）

A、a＞0，b＞0 B、a＞0，b＜0 C、a＜0，b＞0 D、a＜0，b＜0

查看试题解析
3. 下列说法错误的是（）

A、一组邻边相等的四边形是菱形 B、对角线互相垂直的四边形，顺次连接其四边的中点，所得四边形是矩形 C、若三角形的三边长的比为5∶12∶13，则这个三角形是直角三角形 D、若 $\sqrt{a^{2}} = a$ ，则a≥0

查看试题解析
4. 已知一组数据 $x_{1} ， x_{2} ， x_{3} ， x_{4} ， x_{5}$ 的平均数是4，方差是6，则 $3 x_{1} + 4 ， 3 x_{2} + 4 ， 3 x_{3} + 4$ ， $3 x_{4} + 4 ， 3 x_{5} + 4$ 的平均数和方差分别为（）

A、4和6 B、16和6 C、4和22 D、16和54

查看试题解析
5. 同一直角坐标系中，一次函数y＝kx＋b与正比例函数y＝2x的图象如图所示，则不等式kx＋b≥2x的解集为（）

A、x≤－2 B、x＜－2 C、x≥－2 D、x＞－2

查看试题解析
6. 如图的网格中，每个小正方形的边长为1，A，B，C三点均在格点上，结论错误的是（）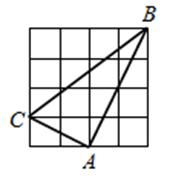

A、AB=2 $\sqrt{5}$ B、∠BAC=90° C、 $S_{� ABC} = 10$ D、点A到直线BC的距离是2

查看试题解析
7. 如图，AC是菱形ABCD的对角线，P是AC上一个动点，过点P分别作AB、BC的垂线，垂足分别是F和E ．若菱形ABCD的周长是12cm，面积是6cm² ，则PE＋PF的值是（）

A、1.5 B、1 C、2 D、4

查看试题解析
8. 一条公路旁依次有 $A ， B ， C$ 三个村庄，甲乙两人骑自行车分别从 $A$ 村、 $B$ 村同时出发前往 $C$ 村，甲乙之间的距离 $s (k m)$ 与骑行时间 $t (h)$ 之间的函数关系如图所示，下列结论：① $A ， B$ 两村相距10 $k m$ ；②出发1.25 $h$ 后两人相遇；③甲每小时比乙多骑行8 $k m$ ；④相遇后，乙又骑行了15 $\min$ 或65 $\min$ 时两人相距2 $k m$ .其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，P为边长为2的正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF.给出以下4个结论：①AP=EF；②AP⊥EF；③EF最短长度为 $\sqrt{2}$ ；④若∠BAP=30°时，则EF的长度为2.其中结论正确的有（）

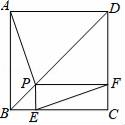A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析
10. 如图，矩形ABCD的面积为20cm² ，对角线交于点O；以AB、AO为邻边作平行四边形 $A O C_{1} B$ ，对角线交于点 $O_{1}$ ，以 $A B ， A O_{1}$ 为邻边作平行四边形 $A O_{1} C_{2} B$ ，对角线交于点 $O_{2}$ ，…，以此类推，则平行四边形 $A O_{n} C_{n + 1} B$ 的面积为（）cm²

A、 $\frac{5}{2^{n - 2}}$ B、 $\frac{5}{2^{n - 1}}$ C、 $\frac{5}{2^{n}}$ D、 $\frac{5}{2^{n + 1}}$

查看试题解析

二、填空题

11. 若最简二次根式 $\sqrt{a}$ 与 $- 3 \sqrt{2 a - 5}$ 能够合并，则a=.

查看试题解析
12. 小明同学用 $S^{2} = \frac{1}{10} [{(x_{1} - 8)}^{2} + {(x_{2} - 8)}^{2} + \dots + {(x_{10} - 8)}^{2}]$ 计算一组数据 $x_{1} ， x_{2} ， \dots ， x_{10}$ 方差，那么 $x_{1} + x_{2} + \dots + x_{10} =$ ．

查看试题解析
13. 如图，在平行四边形ABCD中，BE平分∠ABC ， CF⊥BE ，连接AE ， O为AB的中点，连接OF ，若AE＝4，则OF＝．

查看试题解析
14. 1号探测气球从海拔5m处出发，与此同时2号探测气球从海拔15m处出发，两个气球所在位置的海拔y（单位：m）关于上升时间x（单位：min）的函数关系如图所示，当上升min时，两球之间的距离是5m．

查看试题解析

三、解答题

15. 计算：

(1)、 $| 1 - \sqrt{3} | + {(π - 3)}^{0} - \frac{1}{4} \sqrt{48}$

(2)、 $\sqrt{2} \times (\sqrt{2} + \frac{1}{\sqrt{2}}) - \frac{\sqrt{18} - \sqrt{8}}{\sqrt{2}} + {(\sqrt{2} - 1)}^{2}$

查看试题解析
16. 先化简，再求值： $(a - \frac{2 a - 1}{a}) \div \frac{1 - a^{2}}{a^{2} + a}$ ，其中 $a = \sqrt{3} - 1$ ．

查看试题解析
17. 如图，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．

(1)、在图1中作出平行四边形ABCD ，且点B、D都在小正方形的顶点上，并直接写出四边形ABCD的周长为 ▲ ；

(2)、在图2中作出一个以线段AC为对角线、面积为6的矩形ABCD ，且点B、D都在小正方形的顶点上．

查看试题解析
18. 如图，在△ABC中，AB＝100，BC＝125，AD⊥BC ，垂足为点D ， AD＝60，点A在直线MN上．

(1)、求AC的长；

(2)、若∠MAC＝48°，求∠NAB的度数．

查看试题解析
19. 如图，已知直线 $l_{1} ： y = x + 3$ 与过点A（3，0）的直线 $l_{2}$ 交于点C（1，m），且与x轴交于点B ，与y轴交于点D．

(1)、求直线 $l_{2}$ 的解析式；

(2)、若点D关于x轴的对称点为P ，求△PBC的面积．

查看试题解析
20. 甲乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9

乙：5，9，7，10，9

(1)、填表

平均数

众数

中位数

方差

甲

8

8

0.4

乙

8

9

(2)、从统计的角度分析：教练根据此次成绩，选择甲参加射击比赛，其理由是什么？

(3)、若乙再射击1次，且命中8环，则其射击成绩的方差．（填“变大”“变小”或“不变”）

查看试题解析
21. 如图，平行四边形ABCD中，对角线AC和BD交于点O ，过点A作AE⊥BC于点E ，延长BC到点F ，使CF＝BE ，连接DF和OF ．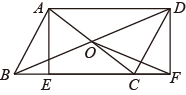

(1)、求证：四边形AEFD是矩形；

(2)、若AD＝5，CE＝3，∠ABF＝60°，求OF的长．

查看试题解析
22. 某果农为响应国家乡村振兴战略的号召，计划种植苹果树和桔子树共100棵．若种植30棵苹果树，70颗桔子树，共需投人成本9200元，若种植30棵桔子树，70棵苹果树，共需投入成本10800元．

(1)、求种植苹果树和桔子树每棵各需投入成本多少元？

(2)、若苹果树的种植棵数不少于桔子树的 $\frac{3}{5}$ ，且总成本投入不超过9710元，问共有几种种植方案？

(3)、在（2）的条件下已知平均每棵苹果树可产30千克苹果，售价为10元/kg，平均每棵桔子树可产25千克桔子，售价为8元/kg，问该果农怎样选择种植方案才能使所获利润最大，最大利润为多少元？

查看试题解析
23. 阅读理解：在平面直角坐标系中，任意两点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ ，则①AB两点的距离＝ $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ ；②线段AB的中点坐标为 $(\frac{x_{1} + x_{2}}{2} ， \frac{y_{1} + y_{2}}{2})$ 解决问题：
如图，平行四边形ABCD中，点B在x轴负半轴上，点D在第一象限，A ， C两点的坐标分别为（0，4），（3，0），边AD的长为6．

(1)、若点P是直线AD上一动点，当PO＋PC取得最小值时，求点P的坐标及PO＋PC的最小值；

(2)、已知直线l：y＝kx＋b过点（0，－2），且将平行四边ABCD分成面积相等的两部分，求直线l的解析式；

(3)、若点N在平面直角坐标系内，在x轴上是否存在点F ，使以A、C、F、N为顶点的四边形为菱形？若存在，请直接写出点F的坐标，若不存在，请说明理由．

查看试题解析

	平均数	众数	中位数	方差
甲	8	8		0.4
乙	8		9