青海省2021年中考数学试卷
试卷更新日期:2021-07-15 类型:中考真卷
一、单选题
-
1. 若 ,则实数 在数轴上对应的点的位置是( ).A、
 B、
B、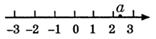 C、
C、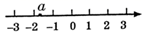 D、
D、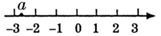 2. 一个两位数,它的十位数字是 ,个位数字是 ,那么这个两位数是( ).A、 B、 C、 D、3. 已知 , 是等腰三角形的两边长,且a,b满足 ,则此等腰三角形的周长为( ).A、8 B、6或8 C、7 D、7或84. 如图所示的几何体的左视图是( ).
2. 一个两位数,它的十位数字是 ,个位数字是 ,那么这个两位数是( ).A、 B、 C、 D、3. 已知 , 是等腰三角形的两边长,且a,b满足 ,则此等腰三角形的周长为( ).A、8 B、6或8 C、7 D、7或84. 如图所示的几何体的左视图是( ). A、
A、 B、
B、 C、
C、 D、
D、 5.
5.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
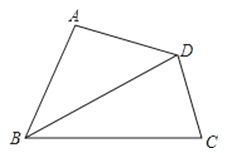 A、7.5 B、8 C、15 D、无法确定6. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于 , 两点,他测得“图上”圆的半径为10厘米, 厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
A、7.5 B、8 C、15 D、无法确定6. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于 , 两点,他测得“图上”圆的半径为10厘米, 厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ). A、1.0厘米/分 B、0.8厘米分 C、12厘米/分 D、1.4厘米/分7. 如图,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只羊 (羊在草地上活动),那么羊在草地上的最大活动区域面积是( )平方米.
A、1.0厘米/分 B、0.8厘米分 C、12厘米/分 D、1.4厘米/分7. 如图,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只羊 (羊在草地上活动),那么羊在草地上的最大活动区域面积是( )平方米.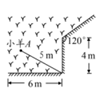 A、 B、 C、 D、8. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、
A、 B、 C、 D、8. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、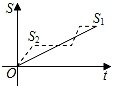 B、
B、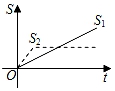 C、
C、 D、
D、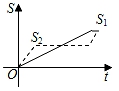
二、填空题
-
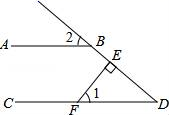
9. 已知 是一元二次方程 的一个根,则代数式 的值等于 .10. 5月11日,第七次人口普查结果发布.数据显示,全国人口共14.1178亿人,同2010年第六次全国人口普查数据相比,我国人口10年来继续保持低速增长态势.其中数据“14.1178亿”用科学记数法表示为 .11. 已知单项式 与 是同类项,则m+n= .12. 已知点 在第四象限,则m的取值范围是 .13. 已知点 和点 在反比例函数 的图象上,则 与 的大小关系是 .14. 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是.
 15. 如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2 , ∠AOB=120°,则图中阴影部分的面积为 .
15. 如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2 , ∠AOB=120°,则图中阴影部分的面积为 . 16. 点 是非圆上一点,若点 到 上的点的最小距离是 ,最大距离是 ,则 的半径是 .17. 如图,在 中, , , 分别是边 , , 的中点,若 的周长为10,则 的周长为 .
16. 点 是非圆上一点,若点 到 上的点的最小距离是 ,最大距离是 ,则 的半径是 .17. 如图,在 中, , , 分别是边 , , 的中点,若 的周长为10,则 的周长为 .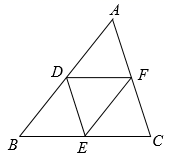 18. 如图,在 中,对角线 , ,垂足为 ,且 , ,则 与 之间的距离为 .
18. 如图,在 中,对角线 , ,垂足为 ,且 , ,则 与 之间的距离为 .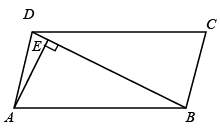 19. 如图,正方形 的边长为8, 是 边上一点,且 , 是对角线 上一动点,则 的最小值为.
19. 如图,正方形 的边长为8, 是 边上一点,且 , 是对角线 上一动点,则 的最小值为. 20. 观察下列各等式:① ;② ;③ …根据以上规律,请写出第5个等式: .
20. 观察下列各等式:① ;② ;③ …根据以上规律,请写出第5个等式: .三、解答题
-
21. 先化简,再求值: ,其中 .22. 如图, 是 的对角线.
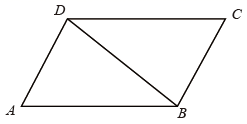 (1)、尺规作图(请用2B铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).(2)、试判断四边形 的形状并说明理由.23. 如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过点 作 于点 ,交 的延长线于点 ,过点 作 于点 .
(1)、尺规作图(请用2B铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).(2)、试判断四边形 的形状并说明理由.23. 如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过点 作 于点 ,交 的延长线于点 ,过点 作 于点 .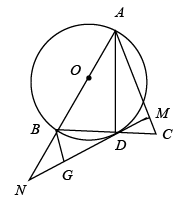 (1)、求证: ;(2)、求证:直线 是 的切线.24. 如图1是某中学教学楼的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ),将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据 , , ).
(1)、求证: ;(2)、求证:直线 是 的切线.24. 如图1是某中学教学楼的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ),将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据 , , ).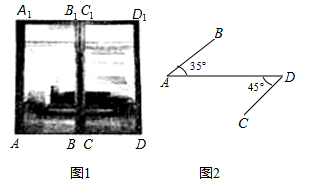 25. 为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:
25. 为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:月平均用水量(吨)
3
4
5
6
7
频数(户数)
4
9
10
7
频率
0.08
0.40
0.14
请根据统计表中提供的信息解答下列问题:
(1)、填空:a= , b= , c= .(2)、这些家庭中月平均用水量数据的平均数是 , 众数是 , 中位数是 .(3)、根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?(4)、市政府决定从月平均用水量最省的甲、乙丙丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.26. 在我们学习过的数学教科书中,有一个数学活动,若身旁没有量角器或三角尺,又需要作 等大小的角,可以采用如下方法:
操作感知:
第一步:对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开(如图13-1).
第二步:再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 (如图13-2).
(1)、猜想论证:
若延长 交 于点 ,如图13-3所示,试判定 的形状,并证明你的结论.(2)、拓展探究:
在图13-3中,若 ,当 满足什么关系时,才能在矩形纸片 中剪出符(1)中的等边三角形 ?27. 如图,在平面直角坐标系中,直线 与坐标轴交于 两点,点 在 轴上,点 在 轴上, 点的坐标为 ,抛物线 经过点 .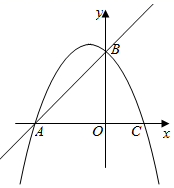 (1)、求抛物线的解析式;(2)、根据图象写出不等式 的解集;(3)、点 是抛物线上的一动点,过点 作直线 的垂线段,垂足为 点,当 时,求P点的坐标.
(1)、求抛物线的解析式;(2)、根据图象写出不等式 的解集;(3)、点 是抛物线上的一动点,过点 作直线 的垂线段,垂足为 点,当 时,求P点的坐标.