广西壮族自治区玉林市北流市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 下列各曲线中,不表示y是 x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一组数据:3、2、4、2、5、3、2,这组数据的众数是( )A、2 B、3 C、4 D、53. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、4. 下列各组数中,能够作为直角三角形的三边长的一组是( )A、1,2,3 B、2,3,4 C、4,5,6 D、3,4,55. 下列计算中正确的是( )A、 B、 C、 D、6. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都是9.3环,方差分别为 , , , ,则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁7. 下列性质中,菱形不具有的是( )A、对边平行且相等 B、对角线互相垂直 C、对角线互相平分 D、对角线相等8. 若点 A(2,y1),B(3,y2)都在一次函数图象 上,则y1与 y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法比较大小9. 如图,菱形 中,对角线 , 相交于点 , 是 边的中点,菱形 的周长为 ,则 的长等于( )
2. 一组数据:3、2、4、2、5、3、2,这组数据的众数是( )A、2 B、3 C、4 D、53. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、4. 下列各组数中,能够作为直角三角形的三边长的一组是( )A、1,2,3 B、2,3,4 C、4,5,6 D、3,4,55. 下列计算中正确的是( )A、 B、 C、 D、6. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都是9.3环,方差分别为 , , , ,则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁7. 下列性质中,菱形不具有的是( )A、对边平行且相等 B、对角线互相垂直 C、对角线互相平分 D、对角线相等8. 若点 A(2,y1),B(3,y2)都在一次函数图象 上,则y1与 y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法比较大小9. 如图,菱形 中,对角线 , 相交于点 , 是 边的中点,菱形 的周长为 ,则 的长等于( )
 A、4 B、8 C、16 D、1810. 在平面直角坐标系中,已知直线y=﹣ x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )A、(0,﹣ ) B、(0, ) C、(0,3) D、(0,4)11. 小元步行从家去火车站,走到6分钟时,以同样的速度回家取物品。然后从家乘出租车赶往火车站.结果比预计步行时间提前了3分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )
A、4 B、8 C、16 D、1810. 在平面直角坐标系中,已知直线y=﹣ x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )A、(0,﹣ ) B、(0, ) C、(0,3) D、(0,4)11. 小元步行从家去火车站,走到6分钟时,以同样的速度回家取物品。然后从家乘出租车赶往火车站.结果比预计步行时间提前了3分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )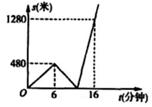 A、1300米 B、1400米 C、1600米 D、1500米12. 如图,在菱形 中, , ,点 、 同时由 、 两点出发,分别沿 、 方向向点 匀速移动(到点 为止),点 的速度为 ,点 的速度为 ,经过 秒 为等边三角形,则 的值为( )
A、1300米 B、1400米 C、1600米 D、1500米12. 如图,在菱形 中, , ,点 、 同时由 、 两点出发,分别沿 、 方向向点 匀速移动(到点 为止),点 的速度为 ,点 的速度为 ,经过 秒 为等边三角形,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
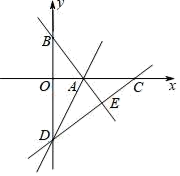
13. 若一组数据2、3、x、4、5的平均数是4,则这组数据的方差为.14. 菱形ABCD中,边长为10,对角线AC=12.则菱形的面积为.15. 若 ,则 的取值范围是.16. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x > k1x+b的解集为
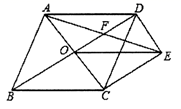
 17. 如图,将矩形纸片 沿直线 折叠,使点 落在 边的中点 处,点 落在点 处,其中 , ,则 的长为 .
17. 如图,将矩形纸片 沿直线 折叠,使点 落在 边的中点 处,点 落在点 处,其中 , ,则 的长为 . 18. 如图,在边长为1的正方形 中, 分别为线段 , 上的点,且 为正三角形,则 的面积为.
18. 如图,在边长为1的正方形 中, 分别为线段 , 上的点,且 为正三角形,则 的面积为.
三、解答题
-
19. 计算:(1)、(2)、20. 已知一次函数 的图象经过点 .
 (1)、求 的值;(2)、求出此函数与两坐标轴的交点坐标,并在此图中画出这个函数的图象;(3)、若该图象与 轴交于点 ,与 轴交于点 ,试确定 的面积.21. 如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
(1)、求 的值;(2)、求出此函数与两坐标轴的交点坐标,并在此图中画出这个函数的图象;(3)、若该图象与 轴交于点 ,与 轴交于点 ,试确定 的面积.21. 如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元? 22. 如图,在平行四边形ABCD中,E、F为对角线BD上的两点,且∠BAF=∠DCE.求证:BE=DF.
22. 如图,在平行四边形ABCD中,E、F为对角线BD上的两点,且∠BAF=∠DCE.求证:BE=DF.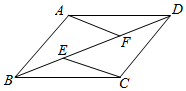 23. 在防疫知识普查考试中,某次测试试题的满分为20分,某校为了解该校部分学生的成绩情况,从该校七,八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析,下面给出了部分信息:
23. 在防疫知识普查考试中,某次测试试题的满分为20分,某校为了解该校部分学生的成绩情况,从该校七,八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析,下面给出了部分信息:抽取的七年级成绩是:20 20 20 20 19 19 19 19 18 18 18 18 18 18 18 17 16 16 15 14
性别
七年级
八年级
平均分
18
18
众数
a
b
中位数
18
c
方差
2.7
2.7

根据以上信息,解答下列问题:
(1)、直接写出上表中a,b,c的值;(2)、在这次测试中,你认为是七年级的成绩好,还是八年级成绩好?请说明理由;(3)、该校七、八年级共有学生1000人,估计此次测试成绩不低于19分的学生有多少人?24. 某校九年级决定购买学习用具对在本次适应性考试中数学成绩进步较大的同学进行奖励,其中计划购买甲、乙两款圆规套装,已知甲款圆规套装所需费用y(元)与购买数量x(套)之间的函数关系如图所示,乙款圆规套装单价为每套11元, (1)、求出y与x的函数关系式;(2)、若购买计划中,甲、乙两款圆规套装共需65套,甲款圆规套装的数量不超过50套,但不少于乙款圆规套装的数量,请设计购买方案,使总费用最低,并求出最低费用.
(1)、求出y与x的函数关系式;(2)、若购买计划中,甲、乙两款圆规套装共需65套,甲款圆规套装的数量不超过50套,但不少于乙款圆规套装的数量,请设计购买方案,使总费用最低,并求出最低费用.