四川省成都市郫都区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期：2021-07-15 类型：期末考试
一、单选题
-
1. 下列图形是公共设施标志，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 如图，两条直线AB，CD交于点O，射线OM是∠AOC的平分线，若∠BOD＝80°，则∠COM的大小为（ ）
A、70° B、60° C、50° D、40°3. 下列计算正确的是（ ）A、（a3）2＝a5 B、a6÷a3＝a2 C、a3•a2＝a6 D、（﹣ab）3＝﹣a3b34. 随着人们对环境的重视，新能源的开发迫在眉睫，石墨烯是现在世界上最薄的纳米材料，其理论厚度应是0.0000034 m，用科学记数法表示0.0000034是（ ）A、0.34×10-5 B、3.4×106 C、3.4×10-5 D、3.4×10-65. 如图，△ABC与△A′B′C′关于直线l对称，若∠A＝50°，∠C＝20°，则∠B'度数为（ ）
A、110° B、70° C、90° D、30°6. 一个不透明的盒子中装有9个白球和1个黑球，它们除了颜色外都相同.从中任意摸出一球，则下列叙述正确的是（ ）.A、摸到白球是必然事件 B、摸到黑球是必然事件 C、摸到白球是随机事件 D、摸到黑球是不可能事件7. 地表以下岩层的温度随着所处深度的变化而变化，在这一问题中自变量是（ ）A、地表 B、岩层的温度 C、所处深度 D、时间8. 如图，工人师傅在安装木制门框时，为防止变形常常钉上两根木条，这样做的依据是（ ）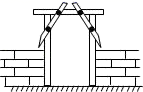
A、三角形具有稳定性 B、两点之间，线段最短 C、直角三角形的两个锐角互为余角 D、垂线段最短9. 若要植一块三角形草坪，两边长分别是20米和50米，则这块草坪第三边长不能为（ ）A、60米 B、50米 C、40米 D、30米10. 如图，BE=CF，AB∥DE，添加下列哪个条件不能证明△ABC≌△DEF的是（ ）
A、AB=DE B、∠A=D C、AC=DF D、AC∥DF二、填空题
-
11. 若二次三项式x2+2mx+81是完全平方式，则常数m的值为.12. 如图，在△ABC中，AB＝AC，BC＝6cm，AD是△ABC的中线，且AD＝5cm，则△ABC的面积为.
13. 如图，三角板直角顶点落在长方形纸片的一边上，∠1＝35°，则∠2＝°.
14. 某人购进一批苹果到市场上零售，已知卖出苹果数量x与售价y的关系如下表.数量x（千克）
1
2
3
4
5
售价y（元）
3+0.1
6+0.2
9+0.3
12+0.4
15+0.5
则当卖出苹果数量为10千克时，售价y为元.
15. 计算：（ ）2019×（ ）﹣2020＝.16. 如图，把一条两边边沿互相平行的纸带折叠，在∠α与∠β的数量关系中，若用∠α的代数式表示∠β，则∠β＝.
17. 有五张正面分别标有数﹣2，0，1，3，4的纸片做成无差别的纸团，洗匀后从中任取一个纸团，若展开后将纸片上的数记为a，则使关于x的方程ax﹣1﹣3（x+1）＝﹣3x的解是正整数的概率为.18. 如图所示，在△ABC中，AB＝6，AC＝4，AD是△ABC的中线，若AD的长为偶数，则AD＝.
19. 如图所示，∠AOB＝60°，点P是∠AOB内一定点，并且OP＝2，点M、N分别是射线OA，OB上异于点O的动点，当△PMN的周长取最小值时，点O到线段MN的距离为.
三、解答题
-
20. 计算：(1)、25×（﹣ ）2﹣4×（﹣ ）0+（ ）-2；(2)、2a（5a﹣4）+（5a+3）（4a﹣2）.21. 先化简，再求值：[（x﹣3y）2+（x﹣2y）（x+2y）﹣x（2x﹣5y）]+（﹣y），其中x＝﹣2，y＝﹣3.22. 根据题意及解答，填注推导理由：
如图，直线AB∥CD，并且被直线EF所截，交AB和CD于点M、N，MP平分∠AME，NQ平分∠CNE.试说明MP∥NQ.
解：∵AB∥CD，
∴∠AME＝∠CNE.（ ）
∵MP平分∠AME，NQ平分∠CNE，
∴∠1＝ ∠AME， ∠CNE.（ ）
∵∠AME＝∠CNE，
∴∠1＝∠2.（ ）
∵∠1＝∠2，
∴MP∥NQ.（ ）
23. 为了准备体育艺术节的比赛，某篮球运动员在进行定点罚球训练，如表是部分训练记录：罚球次数
20
40
60
80
100
120
命中次数
15
32
48
65
80
96
命中频率
0.75
0.8
0.8
0.81
0.8
0.8
(1)、根据上表：估计该运动员罚球命中的概率是；(2)、根据上表分析，如果该运动员在一次比赛中共获得10次罚球机会（每次罚球投掷2次，每命中一次得1分），估计他罚球能得多少分，请说明理由.24. 如图，△ABC中，∠ABC＝30°，∠ACB＝50°，DE、FG分别为AB、AC的垂直平分线，E、G分别为垂足.
(1)、直接写出∠BAC的度数；(2)、求∠DAF的度数，并注明推导依据；(3)、若△DAF的周长为20，求BC的长.25. 如图，AD为△ABC的中线，DE平分∠ADB，DF平分∠ADC，BE⊥DE，CF⊥DF.
(1)、求证；DE⊥DF；(2)、求证：△BDE≌△DCF；(3)、求证：EF∥BC.26. 小明周末外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间，设他从山脚出发后所用的时间为t（分），所走的路程为s（米），s与t之间的函数关系如图所示.
(1)、小明中途休息用了分钟；上述过程中，小明所走的路程为米；(2)、若小明休息后爬山的平均速度是25米/分，求a的值.27.(1)、（知识生成）用两种不同方法计算同一图形的面积，可以得到一个等式，如图1，是用长为a，宽为b（a＞b）的四个全等长方形拼成一个大正方形，用两种不同的方法计算阴影部分（小正方形）的面积，可以得到（a﹣b）2、（a+b）2、ab三者之间的等量关系式：；
(2)、（知识迁移）类似地，用两种不同的方法计算同一个几何体的体积，也可以得到一个等式，如图2，观察大正方体分割，可以得到等式：；
(3)、（成果运用）利用上面所得的结论解答：①已知x+y＝6，xy＝ ，求x﹣y的值；
②已知|a+b﹣6|+（ab﹣7）2＝0，求a3+b3的值.
28. 探究等边三角形“手拉手”问题.
(1)、如图1，已如△ABC，△ADE均为等边三角形，点D在线段BC上，且不与点B、点C重合，连接CE，试判断CE与BA的位置关系，并说明理由；(2)、如图2，已知△ABC、△ADE均为等边三角形，连接CE、BD，若∠DEC＝60°，试说明点B，点D，点E在同一直线上；(3)、如图3，已知点E在ABC外，并且与点B位于线段AC的异侧，连接BE、CE.若∠BEC＝60°，猜测线段BE、AE、CE三者之间的数量关系，并说明理由.