四川省成都市彭州市2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{6}$ B、 $x^{5} + x^{5} = x^{10}$ C、 ${(a b^{4})}^{4} = a^{4} b^{8}$ D、 $a^{10} \div a^{9} = a$

查看试题解析
2. 计算 $2 a^{2} b^{3} \cdot (- 3 a)$ 的结果是（）

A、 $- 6 a^{3} b^{3}$ B、 $6 a^{2} b^{3}$ C、 $6 a^{3} b^{3}$ D、 $- 6 a^{2} b^{3}$

查看试题解析
3. 下列图形是我国国产品牌汽车的标识，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 若x²+mx+9是一个完全平方式，那么m的值是（　　）

A、9 B、±18 C、6 D、±6

查看试题解析
5. 给出下列长度的三条线段，能组成三角形的是（）

A、3 $cm$ ，4 $cm$ ，5 $cm$ B、8 $cm$ ，7 $cm$ ，15 $cm$ C、13 $cm$ ，12 $cm$ ，25 $cm$ D、5 $cm$ ，5 $cm$ ，11 $cm$

查看试题解析
6. 如图，在 $△ A B C$ 中， $B C$ 的垂直平分线分别交 $B C$ ， $A B$ 于点D、E， $B E = 7$ ，则 $C E$ 的长是（）

A、5 B、6 C、7 D、8

查看试题解析
7. 下列事件中，是随机事件的是（）

A、两条线段可以组成一个三角形 B、车辆到达一个路口，遇到红灯 C、若 $a = b$ ，则一定有 $| a | = | b |$ D、度量三角形的内角和是 $360 °$

查看试题解析
8. 新冠肺炎抗疫期间，武汉市公交司机李师傅承担了疫情期间人民医院医生和护士的接送工作，一天到达一个接送点，医生护士们上车后，汽车开始加速，一段时间后又开始匀速行驶，下列图形可以近似地刻画出汽车在这段时间内的速度变化情况的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（）

A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD

查看试题解析
10. 下列说法中，正确的个数有（）
①三角形具有稳定性；

②如果两个角相等，那么这两个角是对顶角；

③三角形的角平分线是射线；

④直线外一点到这条直线的垂线段叫做这点到直线的距离；

⑤任何一个三角形都有三条高、三条中线、三条角平分线；

⑥三角形的三条角平分线交于一点，且这点在三角形内；

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 一个角是 $38 °$ ，则这个角的余角的度数是．

查看试题解析
12. 空气的密度是 $0.001293 g / {cm}^{3}$ ，这个数据用科学记数法表示为 $g / {cm}^{3}$ .

查看试题解析
13. 1-6个月的婴儿生长发育得非常快，在1-6个月内，一个婴儿的体重 $y$ 与月龄 $x$ 之间的变化情况如下表：

月龄/月

1

2

3

4

5

6

体重/克

4700

5400

6100

6800

7500

8200

在这个变化过程中，婴儿的体重y与月龄x之间的关系式是.

查看试题解析
14. 如图，在Rt $△ A B C$ 中， $∠ B = 90 °$ ，在边 $A B$ 、 $A C$ 上分别截取 $A D$ ， $A E$ ，使 $A D = A E$ ，分别以D、E为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在 $∠ B A C$ 内交于点M，作射线 $A M$ 交 $B C$ 边于点F.若 $F B = 2$ ，则点F到 $A C$ 的距离为.

查看试题解析
15. 若 $a b^{3} = - 2$ ，则 $(- 3 a b) \cdot 2 a b^{5} =$ ．

查看试题解析
16. 等腰三角形一腰上的高与另一腰的夹角为50°，则这个等腰三角形的一个底角的度数为．

查看试题解析
17. 如图，从以下给出的四个条件中选取一个：

（ 1 ） $∠ 1 = ∠ 2$ ；

（ 2 ） $∠ 3 = ∠ 4$ ；

（ 3 ） $∠ A = ∠ D C E$ ；

（ 4 ） $∠ A + ∠ A B D = 180 °$ .

恰能判断 $A B$ ∥ $C D$ 的概率是.

查看试题解析
18. 在数学综合与实践课上，老师给出了一组等式： $1 \times 2 \times 3 \times 4 + 1 = {(1^{2} + 3 \times 1 + 1)}^{2}$ ， $2 \times 3 \times 4 \times 5 + 1 = {(2^{2} + 3 \times 2 + 1)}^{2}$ ， $3 \times 4 \times 5 \times 6 + 1 = {(3^{2} + 3 \times 3 + 1)}^{2}$ ， $\cdot \cdot \cdot \cdot \cdot \cdot$ 根据你的观察，则： $n \times (n + 1) \times (n + 2) \times (n + 3) + 1 =$ ．

查看试题解析
19. 如图，在Rt $△ A B C$ 中， $∠ B A C = 90 °$ ， $∠ C = 30 °$ ， $A C = 24$ ， $B D$ 平分 $∠ A B C$ ，点E是 $A B$ 的中点，点F是 $B D$ 上的动点，则 $A F + E F$ 的最小值为.

查看试题解析

三、解答题

20. 计算

(1)、 ${(- \frac{1}{2})}^{- 3} + {(- 3)}^{2} - {(2020 - \frac{2019}{2020})}^{0} + | - 3 |$

(2)、 ${(- \frac{1}{2} a)}^{2} \cdot {(2 a b)}^{2} - a b (a^{3} b - 2 a b^{2})$

查看试题解析
21. 先化简，再求值： $[(x + 2 y) (x - 2 y) + {(2 y + x)}^{2} - 2 x y] \div 2 x$ ，其中： $x 、 y$ 的值满足 ${(x + 2)}^{2} + | y + 3 | = 0$ ．

查看试题解析
22. 如图，现有一个均匀的转盘被平均分成8等份，分别标有2、4、6、8、10、12、14、16这8个数字．转动转盘，当转盘停止时，指针指向的数字即为转出的数字（当指针恰好指在分界线上时，无效，重转）．

(1)、转动转盘，转出的数字是4的倍数的概率是多少；

(2)、小明和小红进行游戏：各自转相同的次数，指针指向3的倍数则小明胜，指针指向4的倍数则小红胜，这个游戏公平吗？为什么？如果让你根据这个转盘来设计一个公平的游戏，你会怎么设计呢？

查看试题解析
23. 如图，在边长为1的小正方形组成的网格中，四边形 $A B C D$ 的四个顶点均在格点上.请按要求完成下列各题：

(1)、在网格中画出四边形 $A B C D$ 关于直线l对称的四边形 $A_{1} B_{1} C_{1} D_{1}$ ；

(2)、求四边形 $A B C D$ 的面积.

查看试题解析
24. 小王家买了一套新房，其结构如图所示（单位：m）．他打算将卧室铺上木地板，其余部分铺上地砖．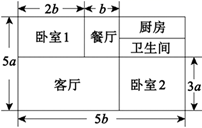

(1)、木地板和地砖分别需要多少平方米？

(2)、如果地砖的价格为每平方米k元，木地板的价格为每平方米2k元，那么小王一共需要花多少钱？

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C = 3$ ， $∠ B = ∠ C = 50 °$ ，点 $D$ 在线段 $B C$ 上运动（点 $D$ 不与点 $B$ ， $C$ 重合），连接 $A D$ ，作 $∠ A D E = 50 °$ ， $D E$ 交线段 $A C$ 于点 $E$ ．

(1)、当 $∠ B D A = 110 °$ 时， $∠ E D C =$ °， $∠ A E D =$ °， $∠ D A E =$ °；

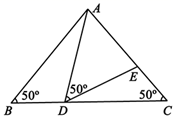(2)、当 $D C$ 等于多少时? $△ A B D$ ≌ $△ D C E$ ，请说明理由．

(3)、在点 $D$ 的运动过程中，请直接写出当 $△ A D E$ 是等腰三角形时 $∠ B D A$ 的度数．

查看试题解析
26. 一个周末上午8：00，小张自驾小汽车从家出发，带全家人去一个4A级景区游玩，小张驾驶的小汽车离家的距离 $y$ (千米)与时间 $t$ (时)之间的关系如图所示，请结合图象解决下列问题：

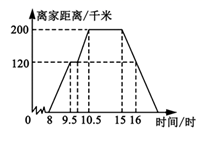(1)、小张家距离景区千米，全家人在景区游玩了小时；

(2)、在去景区的路上，汽车进行了一次加油，之后平均速度比原来增加了20千米 $/$ 时，试求他加油共用了多少小时？

(3)、如果汽车油箱中原来有油25升，平均每小时耗油10升，问小张在加油站至少加多少油才能开回家？

查看试题解析
27.

(1)、已知 $a - b = 2$ ， $a b = 5$ ，求 $a^{2} + b^{2} - 3 a b$ 的值；

(2)、已知 $a^{2} - a - 1 = 0$ ，求 $a^{3} - 2 a^{2} + 3$ 的值.

(3)、如图，有A型、B型、C型三种不同类型的纸板，其中A型是边长为a的正方形，B型是长为a，宽为b的长方形，C型是边长为b的正方形.若想用这些纸板拼成一个长方形，使其面积为 $(a + b) (a + 2 b)$ .
完成下列各题：

①填空 $(a + b) (a + 2 b)$ = ；

②请问需要A型纸板、B型纸板、C型纸板各多少张？试说明理由.

查看试题解析
28.

(1)、如图1， $△ A B C$ 和 $△ D C E$ 都是等边三角形，且B，C，D三点在一条直线上，连接 $A D$ ， $B E$ 相交于点P，求证： $B E = A D$ .

(2)、如图2，在 $△ B C D$ 中，若 $∠ B C D < 120 °$ ，分别以 $B C$ ， $C D$ 和 $B D$ 为边在 $△ B C D$ 外部作等边 $△ A B C$ ，等边 $△ C D E$ ，等边 $△ B D F$ ，连接 $A D$ 、 $B E$ 、 $C F$ 恰交于点P.
①求证： $A D = B E = C F$ ；

②如图2，在（2）的条件下，试猜想 $P B$ ， $P C$ ， $P D$ 与 $B E$ 存在怎样的数量关系，并说明理由.

查看试题解析

月龄/月	1	2	3	4	5	6
体重/克	4700	5400	6100	6800	7500	8200