四川省眉山市青神县2019-2020学年七年级下学期阿数学期末考试试卷

试卷更新日期：2021-07-15 类型：期末考试

进入出卷网下载

一、单选题

1. 方程 $3 + x = 1$ 的解为（）

A、2 B、 $4$ C、 $- 3$ D、 $- 2$

查看试题解析
2. 不等式 $1 - 2 x > 3$ 解集是（）

A、 $x > - 2$ B、 $x < - 1$ C、 $x > - 1$ D、 $x < - 2$

查看试题解析
3. 下列四组数值中，是方程 $3 x - y = 2$ 的解的是（）

A、 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ B、 ${\begin{matrix} x = - 1 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = - 2 \\ y = - 4 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 4 \end{matrix}$

查看试题解析
4. 一个多边形的每一个内角都等于120°，则它的内角和为（　　）

A、540° B、720° C、900° D、1080°

查看试题解析
5. 若 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是方程 $a x - 3 y = 1$ 的一个解，则 $a 的值是$ （）

A、 $7$ B、2 C、 $- 1$ D、 $- 5$

查看试题解析
6. 一个三角形的三边长分别为2，5，x，若x是奇数，则x的值是（）

A、 $5$ B、 $4$ C、 $3$ D、 $6$

查看试题解析
7. 如果 $| x - 2 y + 1 | + | x + y - 5 | = 0$ ，则x、y的值分别是（）

A、 ${\begin{matrix} x = - 1 \\ y = 0 \end{matrix}$ B、 ${\begin{matrix} x = 1 \\ y = 4 \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$

查看试题解析
8. 正方形的对称轴有（）

A、1条 B、2条 C、3条 D、4条

查看试题解析
9. 如图，点E是矩形 $A B C D$ 的边 $D C$ 上一点，把 $△ A D E$ 沿直线 $A E$ 翻折，得到 $△ A E F$ ，若 $∠ B A F = 30^{\circ}$ ，则 $∠ C E F =$ （）

A、 $75 °$ B、 $60 °$ C、 $45 °$ D、 $30 °$

查看试题解析
10. 现有正三角形、正方形、正六边形、正八边形地砖，若只能选择一种地砖铺设地面，则可供选择的地砖有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
11. 如图，以正方形的各边为直径作半圆，若将该图形绕其中心旋转一定角度与原图形重合，则旋转角的最小度数是（）

A、45° B、90° C、135° D、180°

查看试题解析
12. 若不等式组 ${\begin{matrix} 5 - x > 2 \\ 2 x + 3 > 0 \end{matrix}$ 的最小整数解是a，最大整数解是b，则 $a + b =$ （）

A、2 B、 $1$ C、4 D、 $0$

查看试题解析

二、填空题

13. 把方程2x﹣y=1化为用含x的代数式表示y的形式：y=.

查看试题解析
14. 已知a，b满足方程组 ${\begin{array}{l} a + 5 b ＝ 12 \\ 3 a - b ＝ 4 \end{array}$ ，则a+b的值为

查看试题解析
15. 一个等腰三角形的边长分别是3和6，则其周长是.

查看试题解析
16. 在平行四边形、矩形、菱形、正方形四种图形中，绕着其对角线的交点旋转90度，能够和原图形完全重合的有种.

查看试题解析
17. 填在下面三个田字格内的四个数具有相同的规律，根据此规律，则C =.

查看试题解析
18. 如图，六边形 $A B C D E F$ 是轴对称图形， $C F$ 所在的直线是它的对称轴，若 $∠ A F C + ∠ B C F = 150^{\circ}$ ，则 $∠ A F E + ∠ B C D$ 的大小是．

查看试题解析
19. 如图，将Rt△ABC绕点A逆时针旋转70°得到Rt△AB₁C₁ ，若 $∠ C = 90 °$ ， $∠ B = 60 °$ ，则 $∠ BA C_{1} =$ .

查看试题解析
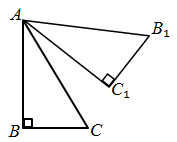20. 已知： $2 + \frac{2}{3} = 2^{2} \times \frac{2}{3} ， 3 + \frac{3}{8} = 3^{2} \times \frac{3}{8} ， 4 + \frac{4}{15} - 4^{2} \times \frac{4}{15} ， 5 + \frac{5}{24} = 5^{2} \times \frac{5}{24}$ ， ……，若 $10 + \frac{b}{a} = 10^{2} \times \frac{b}{a}$ 符合前面式子的规律，则 a + b = .

查看试题解析

三、解答题

21. 解方程： $3 - 2 x = \frac{x + 2}{3}$

查看试题解析
22. 解方程组： ${\begin{matrix} \end{matrix} \begin{matrix} x + y = 3 \\ 3 x - y = 5 \end{matrix}$

查看试题解析
23. 解不等式组 ${\begin{matrix} 4 x - 5 < 3 (x - 1) \\ 2 - \frac{x + 4}{3} > x \end{matrix}$ ，并将解集在数轴上表示出来.

查看试题解析
24. 解方程组： ${\begin{matrix} x + y - z = 4 \\ 2 x - 2 y + z = - 3 \\ 3 x + y - 2 z = 7 \end{matrix}$

查看试题解析
25. 如图，方格纸上每个小正方形的边长均为1个单位长度，△ABC的三个顶点都在格点上（两条网格线的交点叫格点）.

（ 1 ）请在图中画出以MN为对称轴，△ABC的对称三角形 $A_{1} B_{1} C_{1}$ ；

（ 2 ）如果要在对称轴MN上找一点H，使H点到A、B两点的距离之和最短，请在MN上标出点H.

（ 3 ）试计算△ABC的面积.

查看试题解析
26. 如图 $A B / / C D$ ， $∠ A = 100 °$ ， $∠ C = 70 °$ ， $∠ 1 ： ∠ 2 = 5 ： 7$ ，求 $∠ B$ 的度数.

查看试题解析
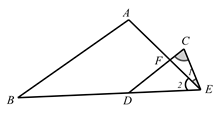27. 某企业接到任务，须在规定时间内生产一批帐篷.如果按原来的生产速度，每天生产120顶帐篷，那么在规定时间内只能完成任务的90%.为按时完成任务，该企业所有人员都支援到生产第一线，这样，每天能生产160顶帐篷，刚好提前一天完成任务.问规定时间是多少天？生产任务是多少顶帐篷？

查看试题解析
28. 观察以下等式：
第1个等式： $\frac{2}{1} = \frac{1}{1} + \frac{1}{1}$ ，

第2个等式： $\frac{2}{3} = \frac{1}{2} + \frac{1}{6}$ ，

第3个等式： $\frac{2}{5} = \frac{1}{3} + \frac{1}{15}$ ，

第4个等式： $\frac{2}{7} = \frac{1}{4} + \frac{1}{28}$ ，

第5个等式： $\frac{2}{9} = \frac{1}{5} + \frac{1}{45}$ ，     ……

按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出第100个等式：；

(3)、写出你猜想的第n个等式：（用含n的等式表示）.

查看试题解析
29. 某文具店准备购进甲，乙两种铅笔，若购进甲种钢笔100支，乙种铅笔50支，需要1000元，若购进甲种钢笔50支，乙种钢笔30支，需要550元.

(1)、求购进甲，乙两种钢笔每支各需多少元；

(2)、若该文具店准备拿出1000元全部用来购进这两种钢笔，考虑顾客需求，要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍，且不超过乙种钢笔数量的8倍，那么该文具店共有几种进货方案；

(3)、若该文具店销售每支甲种钢笔可获利润2元，销售每支乙种钢笔可获利润3元，在第（2）问的各种进货方案中，哪一种方案获利最大；最大利润是多少元.

查看试题解析