四川省攀枝花市西区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-15 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣0.00000031用科学记数法表示，正确的是（）

A、 $- 0.31 \times 10^{- 6}$ B、 $- 3.1 \times 10^{- 6}$ C、 $- 3.1 \times 10^{- 7}$ D、 $- 3.1 \times 10^{- 8}$

查看试题解析
2. 在代数式 $\frac{1}{5} (1 - x) 、 \frac{4 x}{π - 3} 、 \frac{x^{2} - y^{2}}{2} 、 \frac{1}{x} + x 、 \frac{5 x^{2}}{x}$ 中，分式的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 分式 $\frac{x^{2} - 1}{1 - x}$ 的值等于零，则x的值是（）

A、0 B、-1 C、1 D、2

查看试题解析
4. 在平面直角坐标系中，点P（2，﹣3）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 小明的妈妈经营一家服装店，为了合理利用资金，小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析，决定在这个月的进货中多进某种型号服装，此时小明应重点参考（）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析
6. 关于反比例函数 $y = \frac{2}{x}$ 的图象，下列说法正确的是 $($ )

A、图象经过点 $(1 ， 1)$ B、两个分支分布在第二、四象限 C、当 $x < 0$ 时，y随x的增大而减小 D、两个分支关于x轴成轴对称

查看试题解析
7. 下列命题中，正确的是（）

A、邻边相等的四边形是菱形 B、有一个角是直角的四边形是矩形 C、四个角相等的菱形是正方形 D、两条对角线互相垂直且相等的四边形是正方形

查看试题解析
8. 已知关于x的方程 $\frac{2 x}{x - 2} + \frac{3 - m}{2 - x} = 3$ 会产生增根，则m的值为（）

A、－1 B、1 C、2 D、-2

查看试题解析
9. 函数 $y = \frac{k}{x}$ 图象经过点（－4，6），则下列不在 $y = \frac{k}{x}$ 图象上的点是（）

A、（4，-6） B、（-3，8） C、（3，-8） D、（-8，-3）

查看试题解析
10. 如图，平行四边形ABCD的对角线AC、BD相交于O，EF过点O与AD、BC分别相交于E、F.若AB＝4，BC＝5，OE＝1.5，那么四边形EFCD的周长为（）

A、16 B、14 C、10 D、12

查看试题解析
11. 如图，点A是反比例函数 $y = - \frac{6}{x}$ （x＜0）的图象上的一点，过点A作平行四边形ABCD，使B，C在x轴上，点D在y轴上，则平行四边形ABCD的面积为（）

A、1 B、3 C、6 D、12

查看试题解析
12. 如图，在矩形ABCD中，AB＝6，AD＝8，P是AD上不与A和D重合的一个动点，过点P分别作AC和BD的垂线，垂足为E、F，求PE+PF的值是（）

A、10 B、4.8 C、6 D、5

查看试题解析

二、填空题

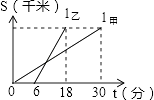
13. 甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．图中l_甲、l_乙分别表示甲、乙两人前往目的地所行驶的路程S（千米）随时间t（分）变化的函数图象，则每分钟乙比甲多行驶千米．

查看试题解析
14. 一组数据 $8$ ， $8$ ，x， $10$ 的众数与平均数相等，则 $x =$ .

查看试题解析
15. 如图，将菱形纸片ABCD折迭，使点A恰好落在菱形的对称中心O处，折痕为EF.若菱形ABCD的边长为2 cm，∠A=120°，则EF=cm.

查看试题解析
16. 如图，在平面直角坐标系中，点A的坐标为(0，3)，△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′在直线y＝ $\frac{3}{4}$ x上，则点B与其对应点B′间的距离为.

查看试题解析
17. 如图，在平面直角坐标系中，点A（0， $\sqrt{3}$ ）、B（﹣1，0），过点A作AB的垂线交x轴于点A₁ ，过点A₁作AA₁的垂线交y轴于点A₂ ，过点A₂作A₁A₂的垂线交x轴于点A₃…按此规律继续作下去，直至得到点A₂₀₁₇为止，则点A₂₀₁₇坐标为.

查看试题解析
18. 如图，在正方形ABCD中，F是对角线AC上的一点，点E在BC的延长线上，且BF=EF.则下列说法：①BF=DF；②△ADF≌△ABF；③DG＝GE；④S_△BCF＝S_△DCF；⑤∠DFE＝90°其中正确的是(填序号).

查看试题解析

三、解答题

19.

(1)、计算： ${[- {\frac{1}{2}}^{- 1} + | \sqrt{2} - 1 | - {(π - 3.14)}^{0} + \sqrt{16}]}^{2} x + {(- 1)}^{2019} + \frac{1}{2 x + 1}$ ；

(2)、解方程： $\frac{2 x}{x - 2} = 1 - \frac{1}{2 - x}$ .

查看试题解析
20. 先化简，再求值： $(1 + \frac{1}{x - 2}) \div \frac{x^{2} - 2 x + 1}{x^{2} - 4}$ ，其中 $x = - 5$ .

查看试题解析
21. 为了考察甲、乙两种小麦的长势，分别从中抽取5株麦苗，测得苗高（单位：cm）如图表所示：

甲

6

8

9

9

8

乙

10

7

7

7

9

(1)、分别计算两种小麦的平均苗高.

(2)、哪种小麦的长势比较整齐？为什么？

查看试题解析
22. 如图所示，在RtΔABC中，∠ACB＝90°，D，E分别为AB，AC边上的中点，连接DE，将ΔADE绕点E旋转180°得到ΔCFE，连接AF，CD.

(1)、求证四边形ADCF是菱形；

(2)、若BC＝8，AC＝6，求四边形ABCF的周长.

查看试题解析
23. 为绿化校园，某校计划购进A、B两种树苗，共21棵.已知A种树苗每棵90元，B种树苗每棵70元.设购买B种树苗x棵，够买两种树苗所需费用为y元.

(1)、y与x的函数关系式为：；

(2)、若购买B种树苗的数量少于A种树苗的数量，请给出一种费用最省的方案.并求出该方案所需费用.

查看试题解析
24. 如图，在平面直角坐标系中，正比例函数y＝3x与反比例函数y＝ $\frac{k}{x}$ 的图象交于A，B两点，点A的横坐标为2，AC⊥x轴，垂足为C，连接BC.

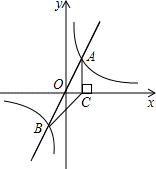(1)、求反比例函数的表达式；

(2)、求△ABC的面积；

(3)、若点P是反比例函数y＝ $\frac{k}{x}$ 图象上的一点，△OPC与△ABC面积相等，请直接写出点P的坐标.

查看试题解析
25. 如图，菱形ABCD的边长为12cm，∠A＝60°，动点P从点A出发，沿着线路AB—BD做匀速运动，动点Q从点D同时出发，沿着线路DC－CB－BA做匀速运动.

(1)、求BD的长.

(2)、已知动点P运动的速度为2cm/s，动点Q运动的速度为2.5cm/s.经过12秒后，P、Q分别到达M、N两点，试判断△AMN的形状，并说明理由.

(3)、设问题（2）中的动点P、Q分别从M、N同时沿原路返回，动点P的速度不变，动点Q的速度改变为acm/s，经过3秒后，P、Q分别到达E、F两点，若△BEF为直角三角形，试求a值.

查看试题解析

甲	6	8	9	9	8
乙	10	7	7	7	9