四川省乐山市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
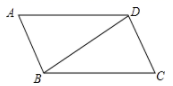
1. 函数 中,自变量x的取值范围是( )A、 B、 C、 D、2. 若一组数据2,x,3,4,5的众数是5,则这组数据的中位数是( )A、2 B、3 C、4 D、53. 某种感冒病毒的直径是0.00000034米,用科学记数法表示为( )A、 B、 C、 D、4. 在直角坐标系中,点 不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,在平行四边形 中, , ,则 的度数为( )
 A、 B、 C、 D、6. 甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )
A、 B、 C、 D、6. 甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )队员
平均成绩
方差
甲
9.7
2.12
乙
9.6
0.56
丙
9.7
0.56
丁
9.6
1.34
A、甲 B、乙 C、丙 D、丁7. 关于直线l:y=kx+k(k≠0),下列说法不正确的是( )A、点(0,k)在l上 B、l经过定点(-1,0) C、当k>0时,y随x的增大而增大 D、l经过第一、二、三象限8. 若 ,则 的值为( )A、 B、 C、 D、9. 如图,将一边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,折痕为PQ,则PQ的长为( )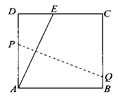 A、12 B、13 C、14 D、1510. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式0<kx+b<2x的解集为( )
A、12 B、13 C、14 D、1510. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式0<kx+b<2x的解集为( ) A、 B、 C、 D、11. 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A、 B、 C、 D、11. 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )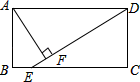 A、△AFD≌△DCE B、AF= AD C、AB=AF D、BE=AD﹣DF12. 如图,点A是函数 图象上一点,连结 交函数 的图象于点B,点C是x轴上一点,且 ,则 的面积为( )
A、△AFD≌△DCE B、AF= AD C、AB=AF D、BE=AD﹣DF12. 如图,点A是函数 图象上一点,连结 交函数 的图象于点B,点C是x轴上一点,且 ,则 的面积为( ) A、2 B、3 C、4 D、6
A、2 B、3 C、4 D、6二、填空题
-
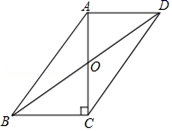
13. 计算: .14. 将直线 向上平移2个单位,得到的直线为.15. 如图,在平行四边形 中, , , .则 .
 16. 小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程 与时间 的图象,则小明回家的速度是每分钟步行m.
16. 小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程 与时间 的图象,则小明回家的速度是每分钟步行m. 17. 如图,边长为3的正方形 绕点C按顺时针方向旋转 后,得到正方形 , 交 于点H,则 .
17. 如图,边长为3的正方形 绕点C按顺时针方向旋转 后,得到正方形 , 交 于点H,则 .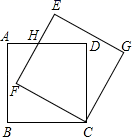 18. 如图1,在四边形 中, , ,点P从点A出发,以每秒1个单位长度的速度,按 的顺序在边上匀速运动.设点P的运动时间为 , 的面积为S,S关于t的函数图象如图2所示.当点P运动到 的中点时, 的面积为.
18. 如图1,在四边形 中, , ,点P从点A出发,以每秒1个单位长度的速度,按 的顺序在边上匀速运动.设点P的运动时间为 , 的面积为S,S关于t的函数图象如图2所示.当点P运动到 的中点时, 的面积为.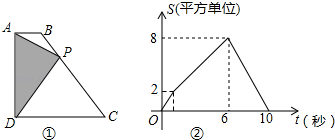
三、解答题
-
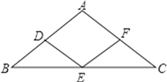
19. 计算: .20. 判断代数式 的值是否能等于1,并说明理由.21. 如图,在△ABC中,AB=AC,四边形ADEF是菱形,求证:BE=CE.
 22. 已知点 在数轴上所对应的数分别为 , ,若 两点关于原点对称.(1)、当 时,求x的值;(2)、若不存在满足条件的x,求m的值.23. 已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
22. 已知点 在数轴上所对应的数分别为 , ,若 两点关于原点对称.(1)、当 时,求x的值;(2)、若不存在满足条件的x,求m的值.23. 已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.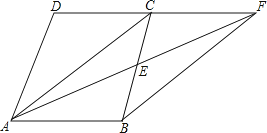 24. 如图,若直线 过点 ,且与x轴交于点A.
24. 如图,若直线 过点 ,且与x轴交于点A.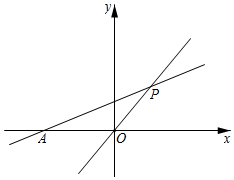 (1)、求直线l的解析式;(2)、若直线 与直线l交于点P,O为原点,求 的面积.25. “新冠肺炎”疫情无疑是对我们每一人的一场生存教育,关注生存环境,就是关注生命.随机抽取某市一年当中若干天的空气质量进行统计分析,其结果如下:
(1)、求直线l的解析式;(2)、若直线 与直线l交于点P,O为原点,求 的面积.25. “新冠肺炎”疫情无疑是对我们每一人的一场生存教育,关注生存环境,就是关注生命.随机抽取某市一年当中若干天的空气质量进行统计分析,其结果如下:空气质量统计表
污染指数( )
40
70
90
110
130
140
天数(t)
3
5
10
8
3
1
频数分布表
分组
40~60
60~80
80~100
100~120
120~140
合计
频数
3
5
10
8
4
频率
0.167
0.333
0.267
0.133
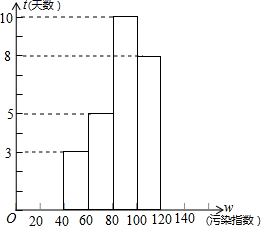
请仔细观察所给的图表,解答下列问题:
(1)、请补全统计图;(2)、如果 时,空气质量为良; 时,空气质量为轻微污染,估计该城市一年(365天)中有多少天空气质量为轻度污染?(3)、请从平均数、众数及中位数三个特征量中,选择你认为适当的一个特征量对该城市一年空气质量的总体情况进行估计和描述,并说明这种估计的合理性.26. 如图,在平面直角坐标系中,直线 与x轴、y轴分别交于点 , .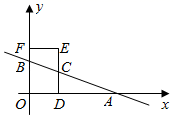 (1)、求直线l的解析式;(2)、若点C为线段 上一动点,过点C作 于点D,延长 至点E,使 ,作 轴于点F,求四边形 的周长.27. 如图, 是边长为3的等边三角形,点D是射线 上的一个动点(点D不与点B、C重合), 是以 为边的等边三角形,过点E作 的平行线,交直线 于点F,连接 .
(1)、求直线l的解析式;(2)、若点C为线段 上一动点,过点C作 于点D,延长 至点E,使 ,作 轴于点F,求四边形 的周长.27. 如图, 是边长为3的等边三角形,点D是射线 上的一个动点(点D不与点B、C重合), 是以 为边的等边三角形,过点E作 的平行线,交直线 于点F,连接 .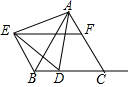 (1)、判断四边形 的形状,并说明理由;(2)、当 时,求四边形 的周长;(3)、四边形 能否是菱形?若可为菱形,请求出 的长,若不可能为菱形,请说明理由.28. 如图,函数 的图象过点 和 两点
(1)、判断四边形 的形状,并说明理由;(2)、当 时,求四边形 的周长;(3)、四边形 能否是菱形?若可为菱形,请求出 的长,若不可能为菱形,请说明理由.28. 如图,函数 的图象过点 和 两点 (1)、求n和k的值;(2)、将直线 沿x轴向左移动得直线 ,交x轴于点D,交y轴于点E,交 于点C,若 ,求直线 的解析式;(3)、在(2)的条件下,第二象限内是否存在点F,使得 为等腰直角三角形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
(1)、求n和k的值;(2)、将直线 沿x轴向左移动得直线 ,交x轴于点D,交y轴于点E,交 于点C,若 ,求直线 的解析式;(3)、在(2)的条件下,第二象限内是否存在点F,使得 为等腰直角三角形,若存在,请直接写出点F的坐标;若不存在,请说明理由.