四川省广安市岳池县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 若关于x的函数 是一次函数,则m的值为( )A、 B、 C、1 D、23. 下列各组数中不是勾股数的是( )A、3,4.5 B、6.8.10 C、5,12.13 D、4,5,64. 若 +(y+2)2=0,则(x+y)2020等于( )A、﹣1 B、1 C、32020 D、﹣320205. 如图,菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=6,BD=8,则OE长为( )
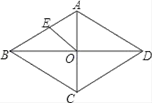 A、3 B、5 C、2.5 D、46. 某地区汉字听写大赛中,10名学生得分情况如下表:
A、3 B、5 C、2.5 D、46. 某地区汉字听写大赛中,10名学生得分情况如下表:分数
50
85
90
95
人数
3
4
2
1
那么这10名学生所得分数的中位数和众数分别是( )
A、85和85 B、85.5和85 C、85和82.5 D、85.5和807. “龟兔首次赛跑”之后,输了比赛的兔子总结惨痛教训后.决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事( 表示乌龟从起点出发所行的时间, 表示乌龟所行的路程, 表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有( )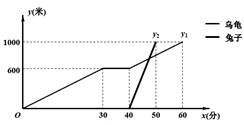 A、1个 B、2个 C、3个 D、4个8. 如图,E是 边 延长线上一点,连接 , , , 交 于点F.添加以下条件,不能判定四边形 为平行四边形的是( )
A、1个 B、2个 C、3个 D、4个8. 如图,E是 边 延长线上一点,连接 , , , 交 于点F.添加以下条件,不能判定四边形 为平行四边形的是( )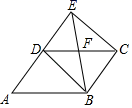 A、 B、 C、 D、9. 若式子 有意义,则一次函数 的图象可能是( )A、
A、 B、 C、 D、9. 若式子 有意义,则一次函数 的图象可能是( )A、 B、
B、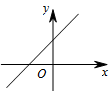 C、
C、 D、
D、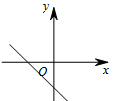 10. 如图,O是菱形 的对角线 的交点,E,F分别是 的中点给出下列结论:① ;②四边形 也是菱形;③四边形 的面积大小等于 ;④ ;⑤是轴对称图形.其中正确的结论有( )
10. 如图,O是菱形 的对角线 的交点,E,F分别是 的中点给出下列结论:① ;②四边形 也是菱形;③四边形 的面积大小等于 ;④ ;⑤是轴对称图形.其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 若二次根式 有意义,则x的取值范围是.12. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD的度数为度.
 13. 长方形ABCD中,AB=6,AD=8,点E是边BC上一点,将△ABE沿AE翻折,点B恰好落在对角线AC上的点F处,则AE的长为 .
13. 长方形ABCD中,AB=6,AD=8,点E是边BC上一点,将△ABE沿AE翻折,点B恰好落在对角线AC上的点F处,则AE的长为 . 14. 如图,正方形 的边长为8, 是 边上一点,且 , 是对角线 上一动点,则 的最小值为.
14. 如图,正方形 的边长为8, 是 边上一点,且 , 是对角线 上一动点,则 的最小值为. 15. 已知将直线 向上平移2个单位后,恰好经过点 ,则不等式 的解集为.16.
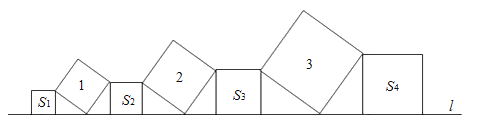
15. 已知将直线 向上平移2个单位后,恰好经过点 ,则不等式 的解集为.16.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+S2+S3+S4=
三、解答题
-
17. 计算: .18. 如图,在由边长为1的小正方形组成的网格中, 的三个顶点均在格点上,请按要求完成下列各题:
 (1)、画线段 且使 ,连接 ;(2)、线段 的长为 , 的长为 , 的长为 , 为三角形.19. 如图所示,根据图中的信息.
(1)、画线段 且使 ,连接 ;(2)、线段 的长为 , 的长为 , 的长为 , 为三角形.19. 如图所示,根据图中的信息.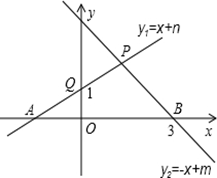 (1)、求m、n的值,(2)、求出P点的坐标,(3)、当 为何值时,20. 如图,在 中,过点D作 于点E,点F在边 上, ,连接 .
(1)、求m、n的值,(2)、求出P点的坐标,(3)、当 为何值时,20. 如图,在 中,过点D作 于点E,点F在边 上, ,连接 .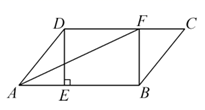 (1)、求证:四边形 是矩形;(2)、已知 是 的平分线,若 ,求 的长度.21. 小明家准备建造长为28米的蔬菜大棚,示意图如图(1).它的横截面为如图(2)所示的四边形 ,已知 米, 米, , , 到 的距离 为1米.矩形棚顶 及矩形 由钢架及塑料薄膜制作,造价为每平方米120元,其它部分(保温墙体等)造价共9250元,则这个大棚的总造价为多少元?(精确到1元)
(1)、求证:四边形 是矩形;(2)、已知 是 的平分线,若 ,求 的长度.21. 小明家准备建造长为28米的蔬菜大棚,示意图如图(1).它的横截面为如图(2)所示的四边形 ,已知 米, 米, , , 到 的距离 为1米.矩形棚顶 及矩形 由钢架及塑料薄膜制作,造价为每平方米120元,其它部分(保温墙体等)造价共9250元,则这个大棚的总造价为多少元?(精确到1元)(下列数据可供参考 )
 22. 钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下.
22. 钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下.收集数据:
甲小区:85,80,95,100,90,95,85,65,75,85,90,90,70,90,100,80,80,90,95,75;
乙小区:80,60,80,95,65,100,90,85,85,80,95,75,80,90,70,80,95,75,100,90.
整理数据:
成绩x/分
甲小区
2
5
a
b
乙小区
3
7
5
5
分析数据:
统计量
平均数
中位数
众数
甲小区
85.75
87.5
c
乙小区
83.5
d
80
应用数据:
(1)、填空: , , , ;(2)、若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;(3)、社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由.23. 在学习习总书记关于生态文明建设重要讲话精神,树立“绿水青山就是金山银山”理念后,某学校计划组织全校1440名师生到某林区植树,经过研究,决定租用当地租车公司一共62辆A,B两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:型号
载客量
租金单价
A
30人/辆
380元/辆
B
20人/辆
280元/辆
注:载客量指的是每辆客车最多可载该校师生的人数.
设学校租用A型号客车x辆,租车总费用为y元.
(1)、求y与x的函数解析式,请直接写出x的取值范围:(2)、若要使租车总费用不超过19600元,一共有几种租车方案?哪种租车方案最省钱?求出最低费用.24. 如图,在 中,点O是 边上的一个动点,过点O作直线 ,设 交 的角平分线于点E,交 的外角 的平分线于点F,连接 .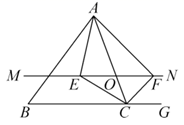 (1)、求证: ;(2)、当点O运动到何处时,四边形 是矩形?并证明你的结论.(3)、在(2)的条件下, 满足什么条件时,四边形 是正方形?并说明理由.25. 定义:在平面直角坐标系中,对于任意两点 , ,若点 满足 , 那么称点T是点A,B的融合点.例如: , ,当点 满足 , 时,则点 是点A,B的融合点.
(1)、求证: ;(2)、当点O运动到何处时,四边形 是矩形?并证明你的结论.(3)、在(2)的条件下, 满足什么条件时,四边形 是正方形?并说明理由.25. 定义:在平面直角坐标系中,对于任意两点 , ,若点 满足 , 那么称点T是点A,B的融合点.例如: , ,当点 满足 , 时,则点 是点A,B的融合点. (1)、已知点 , , ,请说明其中一个点是另外两个点的融合点.(2)、如图,点 ,点 是直线l上任意一点,点 是点D,E的融合点.
(1)、已知点 , , ,请说明其中一个点是另外两个点的融合点.(2)、如图,点 ,点 是直线l上任意一点,点 是点D,E的融合点.①试确定y与x的关系式;
②在给定的坐标系 中,画出①中的函数图象;
③若直线 交x轴于点H.当 为直角三角形时,直接写出点E的坐标.