山西省2020-2021学年高一下学期数学期末考试试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. 已知复数 ,则 ( )A、 B、 C、 D、2. 将圆锥的高缩短到原来的 ,底面半径扩大到原来的2倍,则圆锥的体积( )A、缩小到原来的一半 B、缩小到原来的 C、不变 D、扩大到原来的2倍3. 若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数 , 与函数 , 即为“同族函数”.下而函数解析式中也能够被用来构造“同族函数”的是( )A、 B、 C、 D、4. 甲、乙、丙三人独立地去译一个密码,分别译出的概率为 , , ,则密码能被译出的概率是( )A、 B、 C、 D、5. 数据 , ,…, 的平均数为4,标准差为2,则数据 , ,…, 的方差和平均数分别为( )A、36,14 B、14,36 C、12,19 D、4,126. 设 为实数,已知向量 , .若 ,则向量 与 的夹角的余弦值为( )A、 B、 C、 D、7. 若 , , ,则事件A与B的关系是( )A、互斥 B、相互独立 C、互为对立 D、无法判断8. 如图是函数 ( , )的部分图象,则( )
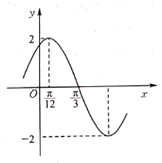 A、函数 的最小正周期为 B、直线 是函数 图象的一条对称轴 C、点 是函数 图象的一个对称中心 D、函数 为奇函数9. 若定义在 上的奇函数 在 上单调递减,且 ,则下列取值范围中的每个x都能使不等式 成立的是( )A、 B、 C、 D、10. 如图,在直三棱柱 中, , , 是 的中一点,点 在 上,记 ,若 平面 ,则实数 的值为( )
A、函数 的最小正周期为 B、直线 是函数 图象的一条对称轴 C、点 是函数 图象的一个对称中心 D、函数 为奇函数9. 若定义在 上的奇函数 在 上单调递减,且 ,则下列取值范围中的每个x都能使不等式 成立的是( )A、 B、 C、 D、10. 如图,在直三棱柱 中, , , 是 的中一点,点 在 上,记 ,若 平面 ,则实数 的值为( ) A、 B、 C、 D、111. 如图所示,在正方体 中,点 , , , 分别为棱 , , , 上的中点,下列判断正确的是( )
A、 B、 C、 D、111. 如图所示,在正方体 中,点 , , , 分别为棱 , , , 上的中点,下列判断正确的是( ) A、直线 平面 B、直线 面 C、平面 平面 D、平面 平面12. 矩形 中, , , 是矩形 内(不含边框)的动点, ,则 的最小值为( )A、 B、 C、 D、
A、直线 平面 B、直线 面 C、平面 平面 D、平面 平面12. 矩形 中, , , 是矩形 内(不含边框)的动点, ,则 的最小值为( )A、 B、 C、 D、二、填空题
-
13. 已知函数 ,则 .14. 已知在 中,点 满足 ,点 在线段 (不含端点 , )上移动,若 ,则 .15. 一组数据共有7个整数, ,2,2,2,10,5,4,且 ,若这组数据的平均数、中位数、众数中最大与最小数之和是该三数中间数字的两倍,则第三四分位数是.16. 如图,在正三棱锥 中,底面边长为 ,侧面均为等腰直角三角形,现该三棱锥的表面上有一动点 ,且 ,则动点 在三棱锥表面所形成的轨迹曲线的长度为.

三、解答题
-
17. 在 中,角 , , 所对的边分别为 , , ,已知 .(1)、求角 ;(2)、若 , 的面积为 ,求 .18. 某药厂测试一种新药的疗效,随机选择1200名志愿者服用此药,结果如下:
治疗效果
病情好转
疗效不明显
病情恶化
人数
800
200
200
(1)、若另一个人服用此药,请估计该病人病情恶化的概率;(2)、现拟采用分层抽样的方法从服用此药的1200名志愿者中抽取6人组成样本,并从这抽出的6人中任意选取3人参加药品发布会,求抽取的3人病情都未恶化的概率.19. 已知向量 , , .(1)、求函数 的单调递增区间和最小正周期;(2)、若当 时,关于 的不等式 有解,求实数 的取值范围.20. 如图,在四棱锥 中, 底面 , , , , , 是 的中点. (1)、求二面角 的大小;(2)、求证: .21. 雪豹处于高原生态食物链的顶端,亦被人们称为“高海拔生态系统健康与否的气压计”.而由于非法捕猎等多种人为因素,雪豹的数量正急剧减少,现已成为濒危物种.在中国,雪豹的数量甚至少于大熊猫.某动物研究机构使用红外线触发相机拍摄雪豹的照片,已知红外线触发相机在它控制的区域内拍摄到雪豹的概率为0.2.(1)、假定有5个红外线触发相机控制某个区域,求雪豹进人这个区域后未被拍摄到的概率;(2)、要使雪豹一旦进人这个区域后有0.9以上的概率被拍摄到,需至少布置几个红外线触发相机( ).22. 如图,已知四棱锥 , 为等边三角形,直线 , , 两两垂直,且 , 为线段 上的一点.
(1)、求二面角 的大小;(2)、求证: .21. 雪豹处于高原生态食物链的顶端,亦被人们称为“高海拔生态系统健康与否的气压计”.而由于非法捕猎等多种人为因素,雪豹的数量正急剧减少,现已成为濒危物种.在中国,雪豹的数量甚至少于大熊猫.某动物研究机构使用红外线触发相机拍摄雪豹的照片,已知红外线触发相机在它控制的区域内拍摄到雪豹的概率为0.2.(1)、假定有5个红外线触发相机控制某个区域,求雪豹进人这个区域后未被拍摄到的概率;(2)、要使雪豹一旦进人这个区域后有0.9以上的概率被拍摄到,需至少布置几个红外线触发相机( ).22. 如图,已知四棱锥 , 为等边三角形,直线 , , 两两垂直,且 , 为线段 上的一点. (1)、若平面 平面 ,求 ;(2)、若三棱锥 的体积为四棱锥 体积的 ,求点 到平面 的距离.
(1)、若平面 平面 ,求 ;(2)、若三棱锥 的体积为四棱锥 体积的 ,求点 到平面 的距离.