湖北省2020-2021学年高一下学期数学7月期末考试试卷
试卷更新日期:2021-07-15 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、 D、2. 在由编号为00,01,02,…,39的40个个体组成的总体中,利用如下的随机数表从第1行第11列开始横向依次选取5个个体组成样本,则选取的第5个个体编号为( )
7816 6572 0802 6314 0702
3204 9243 4935 8200 3623
2976 3413 2481 4241 2424
A、14 B、02 C、32 D、043. 已知向量 , ,若 ,则 ( )A、3 B、 C、 D、4. 新产业工人是推进我国工业化、城镇化发展的主力军,为经济发展做出了重要贡献,近年来国家愈加重视新产业工人群体,出台了各种政策保障新产业工人的合法权益.下图是国家统计局发布的2016-2020年新产业工人规模及增速统计图,则下列说法错误的是( ) A、2020年全国新产业工人总量28560万人,规模约为上年的98.2% B、2017年全国新产业工人增速最大,为1.7%. C、2016-2019年全国新产业工人总量逐年增加 D、2016-2020年全国新产业工人增速逐年增长5. 设 , 为空间内两个不同的平面, 为空间内的一条直线,则下列命题为真命题的是( )A、若 , ,则 B、若 , 则 C、若 , ,则 D、若 , ,则6. 在 中,内角 , , 的对边分别为 , , , , , ,则 的面积为( )A、 B、 C、 D、7. 已知 , 是不共线的向量, , , ,若 , , 三点共线,则实数 的值为( )A、 B、10 C、 D、58. 某宝塔主体是由圆柱、棱柱、球等几何体构成,如图所示.为了测量宝塔的高度 ,某数学兴趣小组在宝塔附近选择楼房 作为参照物,楼房高为 ,在楼顶 处测得地面点 处的俯角为 ,宝塔顶端 处的仰角为 ,在 处测得宝塔顶端 处的仰角为 ,其中 , , 在一条直线上,则该宝塔的高度 ( )
A、2020年全国新产业工人总量28560万人,规模约为上年的98.2% B、2017年全国新产业工人增速最大,为1.7%. C、2016-2019年全国新产业工人总量逐年增加 D、2016-2020年全国新产业工人增速逐年增长5. 设 , 为空间内两个不同的平面, 为空间内的一条直线,则下列命题为真命题的是( )A、若 , ,则 B、若 , 则 C、若 , ,则 D、若 , ,则6. 在 中,内角 , , 的对边分别为 , , , , , ,则 的面积为( )A、 B、 C、 D、7. 已知 , 是不共线的向量, , , ,若 , , 三点共线,则实数 的值为( )A、 B、10 C、 D、58. 某宝塔主体是由圆柱、棱柱、球等几何体构成,如图所示.为了测量宝塔的高度 ,某数学兴趣小组在宝塔附近选择楼房 作为参照物,楼房高为 ,在楼顶 处测得地面点 处的俯角为 ,宝塔顶端 处的仰角为 ,在 处测得宝塔顶端 处的仰角为 ,其中 , , 在一条直线上,则该宝塔的高度 ( )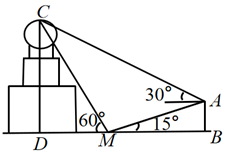 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 下列叙述正确的是( )A、抽样调查具有花费少、效率高的特点 B、数据2,3,9,5,3,9的中位数为7,众数为3和9 C、数据8,9,12,13,15,16,18,20的25%分位数为10.5 D、若将一组数据中的每个数都加上一个相同的正数 ,则平均数和方差都发生变化10. 下列命题是真命题的是( )A、若复数 为纯虚数,则 , B、若复数 为虚数,则 C、若复数 ,则 对应的平面向量为 D、若复数 满足 ,则 的实部与虚部至少有一个为11. 已知平面四边形 , 是 所在平面内任意一点,则下列命题正确的是( )A、若 ,则 是平行四边形 B、若 ,则 是矩形 C、若 ,则 为直角三角形 D、若动点 满足 ,则动点 的轨迹一定通过 的重心12. 如图1,正方形 的边长为2,点 为 的中点,将 沿 所在直线进行翻折,得到四棱锥 ,如图2,则在翻折的过程中,下列命题正确的是( )
 A、点 在某个圆上运动 B、存在某一翻折位置使得 平面 C、存在某一翻折位置使得 平面 D、当二面角 的平面角为 时,四棱锥 的高为
A、点 在某个圆上运动 B、存在某一翻折位置使得 平面 C、存在某一翻折位置使得 平面 D、当二面角 的平面角为 时,四棱锥 的高为三、填空题
-
13. 已知某工厂生产Ⅰ,Ⅱ,Ⅲ三种型号的螺帽,且这三种型号螺帽的周产量之比为 ,现在用分层抽样的方法从某周生产的螺帽中抽取若干个进行质量检查,若抽取Ⅲ型号螺帽25个,则这三种型号螺帽共抽取的个数为.14. 利用斜二测画法得到 的直观图为 ,若 轴, 轴, ,则 的面积为.15. 已知圆柱的高为2,侧面积为 ,若该圆柱的上、下底面圆周都在某一球的球面上,则该球的体积为.16. 已知点 是边长为4的正方形 内部(包括边界)的一动点,点 是边 的中点,则 的最大值是; 的最小值是.

四、解答题
-
17. 质检员为了检测某批1000件产品的质量,随机抽取了100件,检测这些产品的质量指标值(单位:g),依据检测结果将质量指标值按 , , , , 分组,得到如下的频率分布直方图.
 (1)、求这100件产品质量指标值的平均数(同一组中的数据用该区间的中点值作代表);(2)、已知质量指标值在区间 内的为合格品,之外的为不合格品,一件合格品能获利50元,一件不合格品损失30元,试估计这批产品能获利多少元?18. 已知复数 在复平面内对应的点位于第一象限,且 , 是 的共轭复数.(1)、求复数 ;(2)、若 ,求实数 的取值范围.19. 如图所示,在四棱锥 中,底面 是矩形, , .
(1)、求这100件产品质量指标值的平均数(同一组中的数据用该区间的中点值作代表);(2)、已知质量指标值在区间 内的为合格品,之外的为不合格品,一件合格品能获利50元,一件不合格品损失30元,试估计这批产品能获利多少元?18. 已知复数 在复平面内对应的点位于第一象限,且 , 是 的共轭复数.(1)、求复数 ;(2)、若 ,求实数 的取值范围.19. 如图所示,在四棱锥 中,底面 是矩形, , . (1)、若平面 平面 ,证明: ;(2)、若 ,且四棱锥 的体积为 ,求四棱锥 的侧面积.
(1)、若平面 平面 ,证明: ;(2)、若 ,且四棱锥 的体积为 ,求四棱锥 的侧面积.

