上海市黄浦区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中π、 $\frac{1}{6}$ 、﹣ $\sqrt{3}$ 、 $\sqrt{{(- 2)}^{2}}$ 、0.3333……、0.373773……（相邻两个3之间7的个数依次加1个）中，无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 运算中，正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 ${(\sqrt{3} - 2)}^{2} = | \sqrt{3} - 2 |$ C、 $\sqrt{a^{2}} = a$ D、 ${(\sqrt{a + b})}^{2}$ ＝a＋b

查看试题解析
3. 已知面积为10的正方形的边长为 $x$ ，那么 $x$ 的取值范围是（）

A、 $1 < x < 3$ B、 $2 < x < 3$ C、 $3 < x < 4$ D、 $4 < x < 5$

查看试题解析
4. 下列说法正确的是（）

A、如果两个角相等，那么这两个角是对顶角 B、经过一点有且只有一条直线与已知直线平行 C、如果两条直线被第三条直线所截，那么内错角相等 D、联结直线外一点与直线上各点的所有线段中，垂线段最短

查看试题解析
5. 平面直角坐标系中，将点A（﹣3，﹣5）向上平移4个单位，再向左平移3个单位得到点B，则点B的坐标为（）

A、（1，﹣8） B、（1，﹣2） C、（﹣6，﹣1） D、（0，﹣1）

查看试题解析
6. 如图，在△ABC中，点D、E分别在边AB、AC上，BE与CD相交于点O，如果已知∠ABC=∠ACB，补充下列一个条件后，仍无法判定△ABE≌△ACD的是（）

A、AD＝AE B、BE＝CD C、OB＝OC D、∠BDC＝∠CEB

查看试题解析

二、填空题

7. $\sqrt{16}$ 的平方根是．

查看试题解析
8. 比较大小：﹣5 ﹣2 $\sqrt{6}$ （填“＞”，“＝”或“＜”）．

查看试题解析
9. 计算：（ $\sqrt{3}$ ＋2）²×（ $\sqrt{3}$ ﹣2）²＝．

查看试题解析
10. 把 $\sqrt[3]{5^{2}}$ 表示成幂的形式是.

查看试题解析
11. 月球沿着一定的轨道围绕地球运动，某一时刻它与地球相距405 500千米，用科学记数法表示这个数并保留三个有效数字是千米．

查看试题解析
12. 点A（1－a，5 ），B（3，b ）关于y轴对称，则a+b= ．

查看试题解析
13. 如图，在△ABC中，∠C=50°，按图中虚线将∠C剪去后，∠1+∠2等于．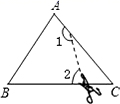

查看试题解析
14. 若 $△$ ABC中，∠A：∠B：∠C=1：1：2则 $△$ ABC的形状是

查看试题解析
15. 如图，在四边形ABCD中，∠C＋∠D＝180⁰ ， ∠A－∠B＝40⁰ ，则∠B＝.

查看试题解析
16. 如图，在△ABC中，AB＝AC，BD＝CE，CD＝BF，若∠A＝50°，则∠EDF的度数为．

查看试题解析
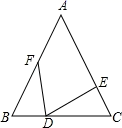17. 已知等腰三角形的两条边长分别是3cm、7cm，那么这个等腰三角形的周长是 cm．

查看试题解析
18. 当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为．

查看试题解析
19. 在等腰△ABC中，如果过顶角顶点A的一条直线AD将△ABC分割成两个等腰三角形，那么∠BAC＝．

查看试题解析
20. 如图，在△ABC中，∠A＝42°，点D是边A上的一点，将△BCD沿直线CD翻折斜到△B′CD，B′C交AB于点E，如果B′D∥AC，那么∠BDC＝度．

查看试题解析

三、解答题

21. 计算： $\sqrt{5} \div \sqrt{2} \times 2 \sqrt{2} \times 2 \sqrt{5}$ ．

查看试题解析
22. 计算：（﹣3）⁰﹣ $\sqrt{27} + {(\sqrt{3} - 1)}^{2} + | 1 - \sqrt{3} |$ ．

查看试题解析
23. 利用幂的运算性质计算： $2 \sqrt{2} \times \sqrt[3]{2} \times \frac{1}{\sqrt[6]{2^{5}}}$ ．

查看试题解析
24. 如图，点A、B、C、D在一条直线上如果AC＝BD，BE＝CF，且BE∥CF，那么AE∥DF．为什么？
解：∵BE∥CF（已知）

∴∠EBC＝∠FCB（    ）

∵∠EBC＋∠EBA＝180°，∠FCB＋∠FCD＝180°（平角的意义）

∴∠EBA＝∠FCD（    ）

∵AC＝BD（已知）

∴AC﹣BC＝BD﹣BC（等式性质），

即    ▲     （完成以下说理过程）

查看试题解析
25. 在直角坐标平面内，已知点A的坐标（﹣1，4），点B的位置如图所示，点C是第一象限内一点，且点C到x轴的距离是2，到y轴的距离是4

(1)、写出图中点B的坐标；

(2)、在图中描出点C，并写出图中点C的坐标：；

(3)、画出△ABO关于y轴的对称图形△A′B′O；

(4)、联结A′B、BB′、B′C、A′C．那么四边形A′BB′C的面积等于

查看试题解析
26. 如图在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠1＝∠2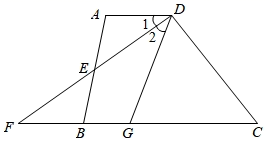

(1)、说明△ADE≌△BFE的理由；

(2)、联结EG，那么EG与DF的位置关系是，请说明理由．

查看试题解析
27. 如图，已知在△ABC中，∠ACB＝90°，AC＝BC，∠A的平分线AD交BC于点D，过点B作BE⊥AD于E．

(1)、说明△ACD≌△BCF的理由；

(2)、BE与AD的长度关系是，请说明理由．

查看试题解析
28. 如图1，以AB为腰向两侧分别作全等的等腰△ABC和△ABD，过顶角的顶点A作∠MAN，使∠MAN＝∠BAC＝α（0°＜α＜60°），将∠MAN的边AM与AC叠合，绕点A按逆时针方向旋转，与射线CB、BD分别交于点E、F．设旋转角度为β．

(1)、如图1，当0°＜β＜α时，说明线段BE＝DF的理由；

(2)、当α＜β＜2α时，在图2中画出正确的图形井写出此时线段CE、FD与线段BD的数量关系是．（直接写出答案）

(3)、联结EF，在∠MAN绕点A逆时针旋转过程中（0°＜β＜2α），当线段AD⊥EF时，用含α的代数式表示∠CEA＝（直接写出答案）．

查看试题解析